High speed development of new chemical synthesis and materials at molecular-level: Methods and approaches

Abstract

Recent success of advanced computational chemistry, in example for the prediction of chemical reactivity and materials properties, reflects its reputation as a valuable and widely accepted means to tackle problems in academia. The development of new simulation methods and new computer architectures enables an enormous improvement of the productivity of research and development of new chemical synthesis and materials. These advances can be achieved in terms of less time, material, and staff compared to traditional lab experiments. Especially, approaches like virtual high throughput screenings (vHTS) are highly scalable and allow fast and deep insights into new promising system modifications. Consequently, the time to market and risk of new product development can be decreased significantly. These characteristics paved the way for the successful application in industry nowadays.

1 Introduction

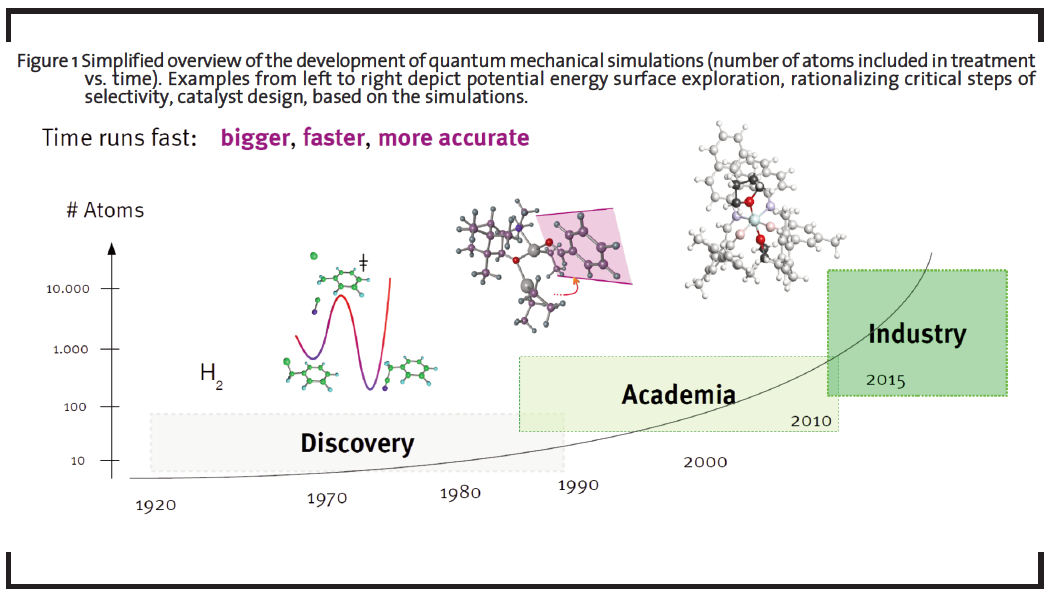
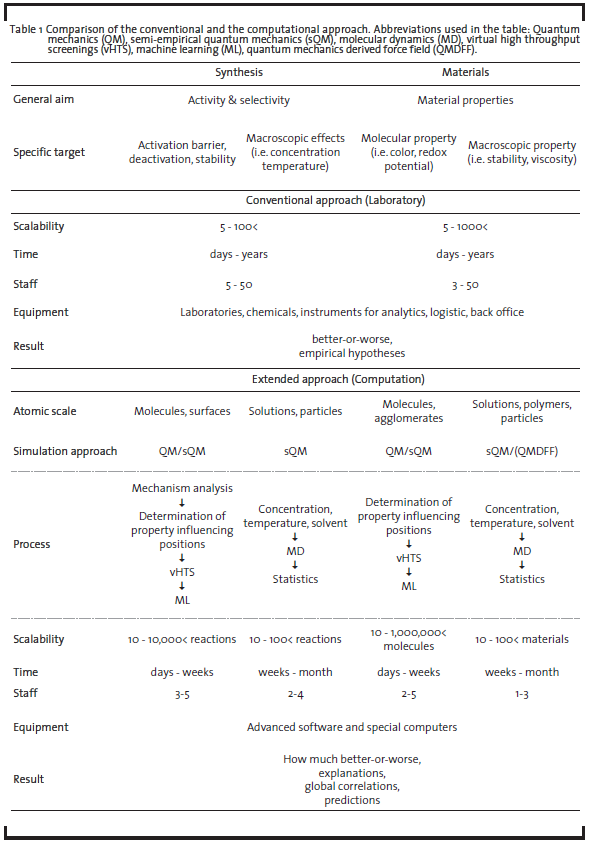
The field of computational chemistry is diverse and offers a number of inherently different approaches suitable for different problems, targeting isolated molecules in the gas phase to extended solids, polymers, and liquids. By simulating not only energy and derivative properties, but adding a time domain to the problem, the dynamics of the system of interest can be accessed. For research and development (R&D) projects, computational chemistry is an ideal tool to test new ideas for chemical transformations and new materials on the molecular level due to the fact that computations do not require synthesis or dedicated lab equipment. Furthermore, experimentally hard to characterize molecules – such as transient intermediates – can be investigated to full detail. In view of these benefits and the moderate investment costs for a specialized interdisciplinary team with own IT-Infrastructure (and no need for laboratory equipment), companies are able to generate a comparatively high return of investment (ROI) through developing new game-changing materials and synthesis routes (see a comparison of characteristics of traditional vs. computationally supported approaches in Table 1). This potential and value of using computational approaches has already been pointed out in several industrial roadmaps (The American Chemical Society, 1996; Council for Chemical Research, 1999; Roadmap for Catalysis Research in Germany, 2010). The significantly increased number of molecules researched by computational chemistry is also schematically demonstrated in Figure 1.

From the vast field of computational chemistry, including multiscale descriptions, low-resolution, “coarse-grained” models, and the broad field of classical molecular dynamics, this article focusses on describing techniques based on quantum mechanics providing universal descriptions of chemical transformations and materials as well as delivering key properties arising from the electronic structure that are not accessible with classical methods. In the following sections, an overview about the prospects and limitations of the technology is given and exemplary fields in which computational approaches have already been successfully applied and yielded in breakthrough innovations are presented. Selected methods and problems are used as showcases, e.g. to demonstrate how quantum chemical investigations can be utilized to analyze a) key steps of chemical processes, b) how strategies for the design of catalysts are adapted and c) how the identification of new materials can be accelerated.

1.1 Application of quantum mechanics: Synthesis

Improving the efficiency of chemical manufacturing processes leads to significant strategic advantages in highly competitive markets, which consequently enables companies to generate a higher added value. If the possibilities of cost reductions by optimizing the application of raw materials and energy supply are exhausted, increased process economy in form of higher production rates or higher product selectivity can be achieved by changing the process itself, additives (e.g. catalyst, ligand) or adjusting reaction conditions (e.g. solvent, temperature, process structure). Since the synthesis of chemical compounds can be a complex multi-step process during which different molecules interact within a particular reaction environment (e.g. solvent, catalysts, pollutants), adjustments of processes can be demanding.
Quantum mechanics offers the possibility to perform simulations for well-defined and designed model systems as well as for model problems picked by the researcher. The individual reaction steps and interactions, which are usually planned, performed, and analyzed in laboratories, can thus be disentangled and examined separately and quantitatively without interference. Then, subsequently increasing the complexity of the simulations, influences of the individual reaction components on the whole process can be determined at the molecular level. In addition, the influence of process parameters such as temperature, polarity, and structure as well as solvent and concentration effects, which are known to have a high impact on the conversion and selectivity of reactions, can be investigated. In addition to stoichiometric syntheses, catalytic reactions can be studied by employing appropriate models for the active center of the catalysts (in fact, catalyzed reactions constitute the major part of chemical production). Using algorithms to search for critical points of the reaction path(s) such as the involved intermediate minima and their liaising transition states assembles a greater picture of the overall mechanism. Its analysis in terms of the energetics and entropic effects helps to determine why a reaction with one specific catalyst is faster and more selective than with a different one. Interpreting the molecular level findings on the process scale can provide evidence of why for example currently used production methods suffer from poor conversion or produce contaminated products, which need to be isolated at a high price. Due to the technically facile scalability of computations and number of mechanistic paths investigated, it is possible to examine a large number of molecular variations and reaction conditions in a short time compared to practical laboratory experiments (weeks instead of years). This saving in time allows for the parallelized exploration of process parameters: tailored to the chemical process and at the same time with high throughput. Table 1 compares the main characteristics of the conventional and extended approach.

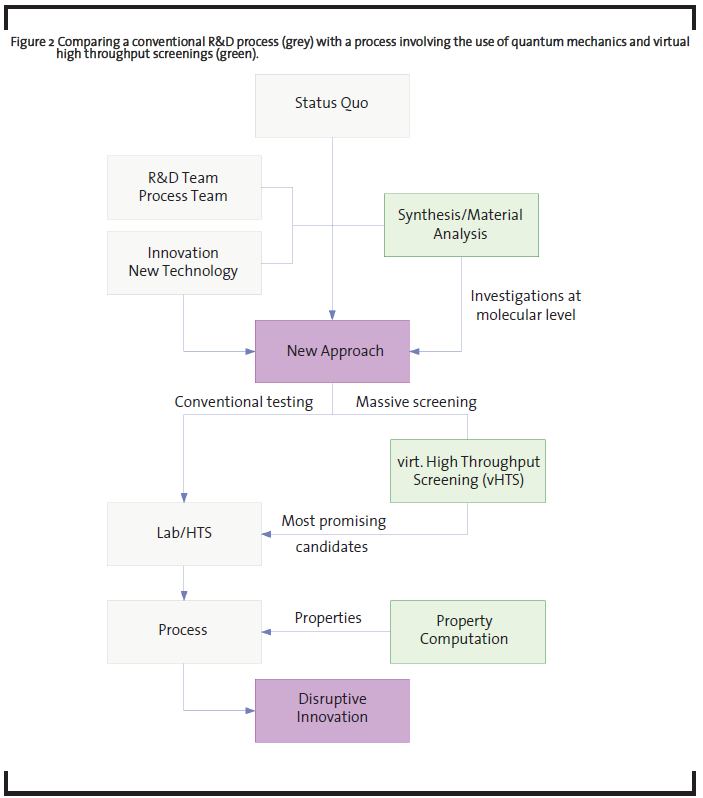
The throughput of the computations can be further accelerated when using chemoinformatics concepts that use data mining and chemical databases techniques and allow high grades of automatization. The interaction with the vHTS scheme in an R&D project, together with a workflow is sketched in Figure 2. The presented example highlights that virtual high-throughput screenings (vHTS) may be used to investigate numerous new variations and to test in the computer model whether target parameters such as yield or selectivity can be improved. Consequently, the gained understanding of the trends in the reaction (especially the role of a series of modified catalysts) and the narrowing of the chemical variation space to only promising candidates greatly reduces development time and costs.

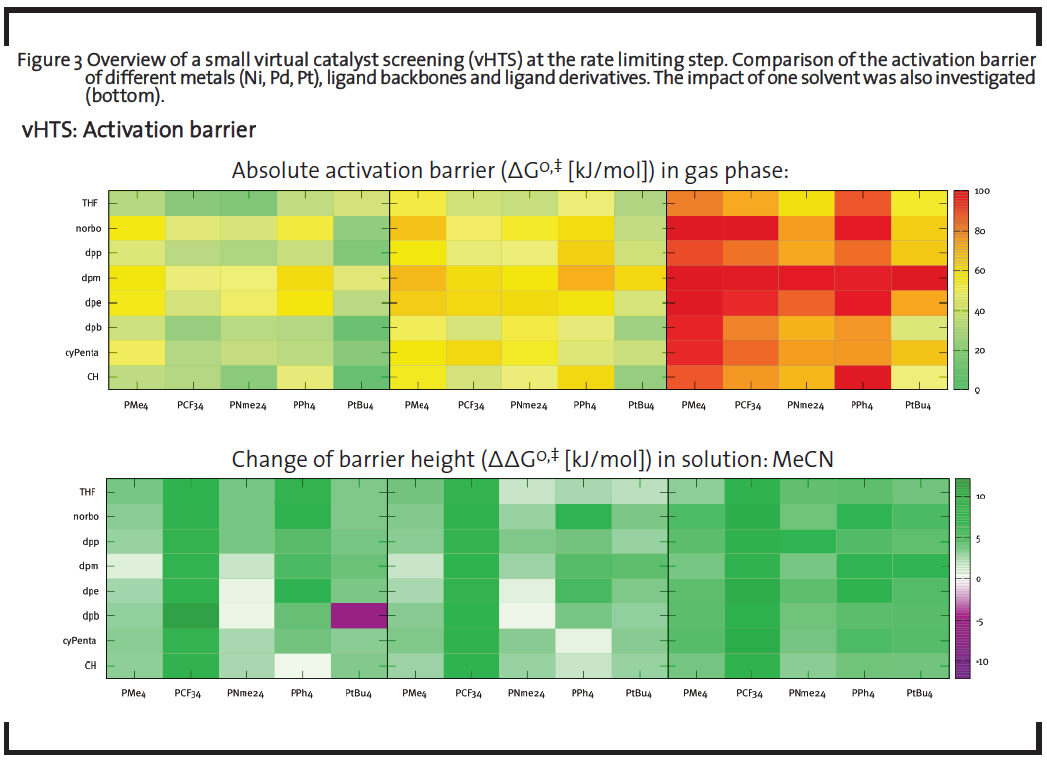
Figure 3 exemplary shows a screening of the activation barrier of a CO insertion reaction, whereby the performance of several metals, ligand backbones, ligand rests, and solvents was evaluated. Homogeneous catalysts derived from Cole-Hamilton-type (metal-organic complexes) were taken as model catalysts. Different modifications were created in-silico by changing functional groups of the ligands extremity (altering the bulkiness of the overall catalyst) and by changing the bidentate ligand’s backbone length (altering the coordination geometry). The CO-insertion barrier was taken as descriptor that significantly contributes to the overall turnover frequency (TOF) of the reaction. For every member, this barrier was calculated at the DFT level (see below) and the height was color-coded. Green entries correspond to catalysts with high TOF – indicating potentially interesting leads for further testing. These quick evaluations thus show clearly which kind of metal, ligand backbone, and ligand rest combination is the most promising.

1.2 Application of quantum mechanics: Materials

The prospect to use theoretical methods to design and test new compounds in silico led to the idea of first-principles materials discovery (Curtarolo et al., 2013; Greeley et al., 2006; Maier et al., 2007). The necessary high-throughput computational screening (explanation see 1.1) of hypothetical chemical motifs or elemental compositions has indeed become more feasible in the recent past, given the availability of scalable high-performance computing infrastructure. Such pre-screening procedure would reduce the R&D costs, where optimization potential of components for display dyes (Figure 4), batteries (Figure 5), sensors, electric circuits, photovoltaic devices, etc. is expected by tuning the chemical structure and composition of the material itself. This can be achieved by choosing few promising backbones and create several derivatives of these structures. Compared to the research in laboratories, modern virtual high throughput screenings can examine much more structures in shorter time periods, at much lower costs, and offering more results per molecule.

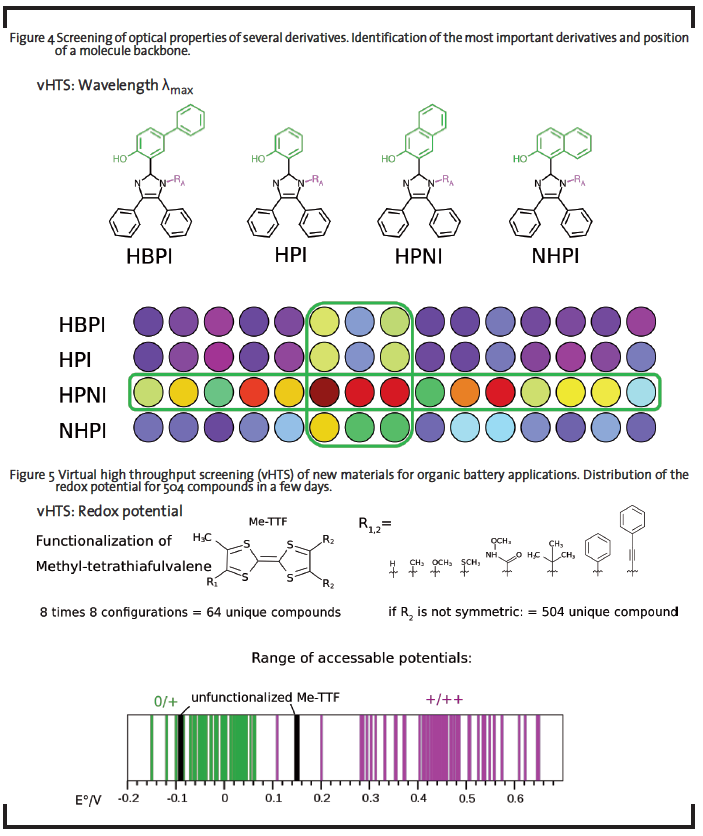
For new OLED emitter materials, one interesting question is to tune the color of the electroluminescence by chemical modification. In the example shown in Figure 4, modifications were done to an imidazole-derived compound displaying interesting photophysics. Known synthetically available modifications constitute the backbones HBPI, HPI, HPNI, and NHPI to be further functionalized at position RA. The screened descriptor is the emission wavelength obtained by a tailored semi-empirical excited state method after excited state relaxation. The values are coded to an RGB value for the visualization. The result from this screening is that only one backbone provides sensitivity to modification at RA, while the others are relatively tolerant. Therefore, only the “sensitive” backbone might be chosen for further treatment, since it covered a broad range of emission properties.
For the development of new organic battery materials, tuning the redox potential of a redox-active agent on the molecular level might be necessary. One interesting redox-active organic motif is based on the tetrathiafulvalene (TTF) moiety. In the example screening in Figure 5, experimentally common functional groups are introduced in silico at three positions to evaluate the impact of modification on the energetics of two oxidation steps (0/+) and (+/++). The reference potentials (see black line) of the unfunctionalized molecule is systematically shifted to higher values as an outcome of the screening, which further allows to estimate the range of potentials addressable by this type of modification (the range covered by green and magenta sticks, respectively, for the two redox stages).
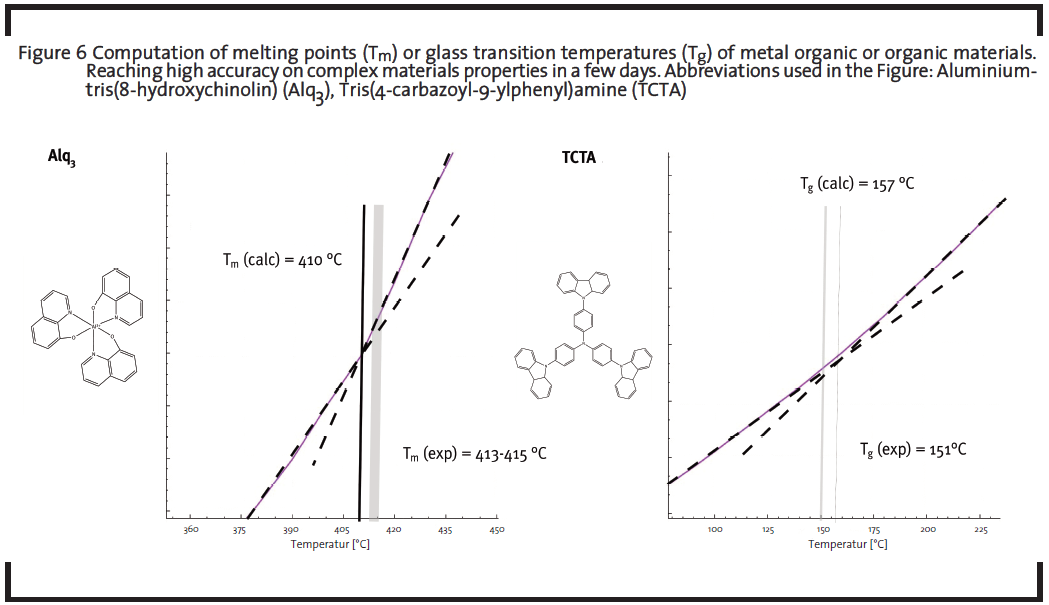
Apart from the conduction of individual simulations within a screening, the time-evolution of the systems’ structure can be simulated. With increasing computational power and advanced methodologies that allow quantum-level accuracy treatment with low computational costs, it is nowadays even possible to predict complex macroscopic properties like melting points or glass transition temperatures of any molecules or molecule mixtures with very low deviations to experiments. Figure 6 shows exemplary the significant changes of the phase around the melting point or glass transition temperature, respectively.

So far, also several industrial players made progress in establishing databases of predicted material properties (Jain et al., 2011). Despite the emerging technical feasibility of performing these screenings, their practical use in materials discovery in an industrial frame is limited so far. This limitation is mostly due to a discrepancy between the practical framework for the development of new materials in the R&D process characterized by safety regulations, costs, compatibility or durability requirement, etc. and the rather limited prospect of a purely theoretically proposed formula to be ultimately successful. To picture an example, platinum metal is still frequently used as electrocatalyst in the hydrogen evolution reaction in water electrolysis, although several computational screenings have proposed materials of other elemental composition (Greeley et al., 2006; Andersson et al., 2006). However, a low number of abstract and simplified theoretical descriptors of the performance are usually screened, so that theoretically expected performance and the practical performance (including stability of the material under load and realistic – harsh conditions) are contrasting. This high number of uncertainties underlines that more tailored screening approaches are of much more practical use, where the screening extends and complements know-how and expertise of researchers who are merely using the computational tools. As for the chemical synthesis, a screening approach as presented in section 1.1 enables to perform a computational screening of compounds, profiting from the expertise in physico-chemistry of the team of researchers. The balanced choice of theoretical descriptors including stability and performance issues as well as environmental factors, realizes a more directed computational screening than a brute-force high-throughput screening. A similar conceptional screening approach can be tailored to the material’s sector as presented in section 1.2. With the established systematic structure-property relationships that are the outcome of such studies, design of materials is greatly facilitated and costs can be reduced by feeding the data in larger-scale models performing device-level simulation to test new ideas in-silico.

2 Simulation methods

Theoretical methods to describe structure and dynamics of materials and chemical compounds on the molecular level encompass classical and quantum mechanics. Molecular dynamics simulations are often based on the former where interactions between the particles are parametrized as bonds, angles, dihedral angles as well as non-bonded (Coulomb and van der Waals interactions), denoted as the force field (see for example (Mackerell, 2004; Ponder and Case, 2003)). Quantum mechanics, on the other hand, provides, a universal way to mathematically describe the properties of matter.
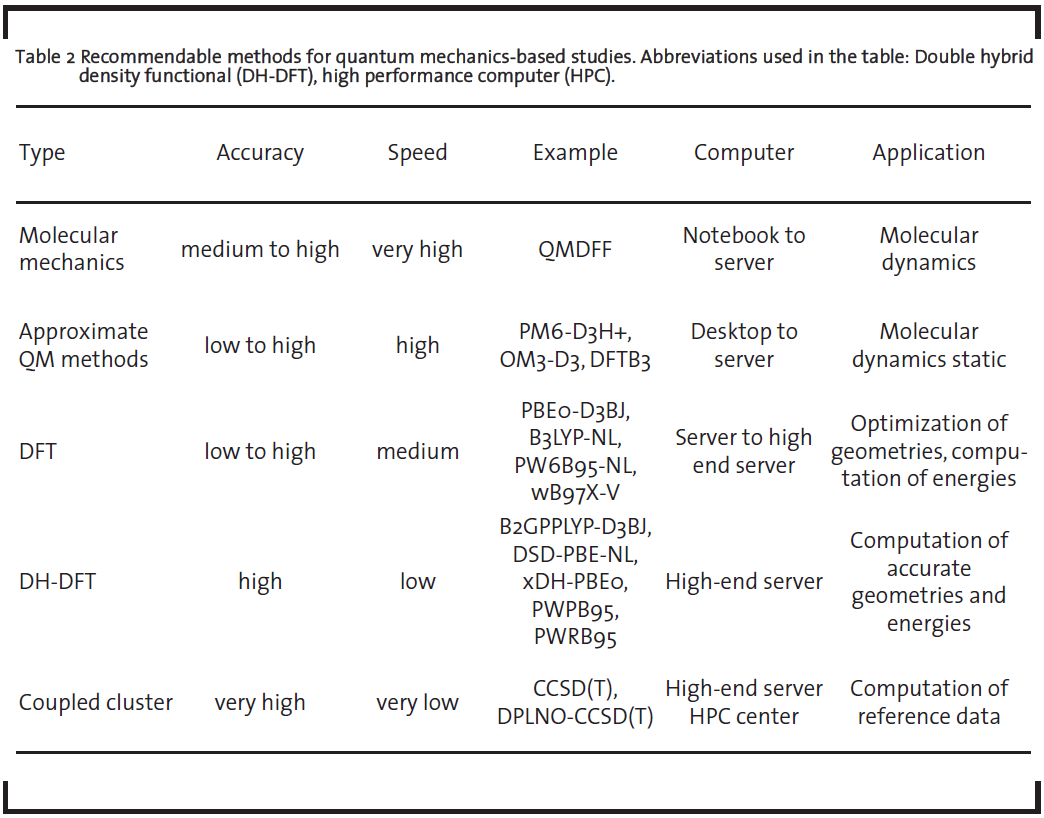
The accurate ab-initio methods solving the Schrödinger equation (like coupled cluster or perturbation theory methods or quantum monte carlo simulation), however, are in view of the high computational costs not very frequently used and their application is so far limited to academic show-cases rather than industry-relevant species. A list of recommendable methods and their characteristics are shown in Table 2.

In contrast to the accurate universal bottom-up quantum description, empirical expressions can be used that represent a chemical species by a predefined topology (connectivity). The simulated molecular dynamics using relatively simple potential functions is attractive to predict the structural behavior, especially of soft matter. The low computational costs allowing to simulate rather long timescales of the dynamics of big systems, with the state of the art being for example a full virus capsid (64 million atoms, 100 ns) (Zhao et al., 2013). The drawback of classical mechanics is its limitation to a single chemical species so that chemical transformations or other processes with a change in electronic structure can only be incorporated with more complicated extensions such as a reactive force field (Van Duin et al., 2001) or the empirical valence bond method (Kamerlin and Warshel, 2011; Warshel and Weiss, 1980). Furthermore, there exist severe limitations in the systems that are well described by current standard parameter sets, especially regarding transitions metals. Addressing this problem, quantum chemistry is of great help. In Grimme’s QMDFF approach, for example, the usual parametrization of representative building blocks by hand is replaced by a tailored system-dependent QM calculation (Grimme, 2014), which can even be applied to rather complicated transition metal complex-containing systems, and still bear all benefits of a classical potential simulation.
This development already points into future directions, where combinations of universal quantum descriptions together with a suitable parametrization to lower the computational costs will be further developed. Incorporation of electron correlation and treating metals will be the challenge for and the advancement of semi-empirical methods exceeding the currently available methods and parametrizations like PM6-D3H+ (Stewart, 2007; Kromann et al., 2014), DFTB3 (Koskinen and Mäkinen, 2009; Gaus et al., 2011).
Intermediate between highly empirically parametrized methods and parameter-free ab-initio quantum chemistry is the density functional theory (DFT) that is the workhorse method in computational chemistry. This method provides high accuracy in many cases on the one hand and manageable computational costs on the other. Because it is impossible to test all available methods regarding the applicability to a given problem, benchmark studies – that is testing a number of methods for a representative class of test-molecules – are often performed to measure their suitability. Although there are a number of benchmarks for a large range of computational tasks, e.g. noncovalent interactions (Burnset al., 2011) and excited states, it is a well-accepted fact, that there exists no all-purpose method that yields acceptable results throughout all phenomena and all classes of molecules. For example, for quite some time, the B3LYP hybrid functional has been regarded as such all-purpose model chemistry, however, in the recent past, the opposite has been proven (Sure and Grimme, 2015; Kruse et al., 2012; Grimme et al., 2010). Often, this functional provides the worst compromise among comparable methods, while well-chosen state-of-the art functionals may operate within the experimental uncertainties. Sometimes, DFT itself fails to qualitatively describe the molecule of interest so that, despite the higher computational costs ab initio approaches have to be chosen.
One direction to overcome inherent errors in the DFT methodology is to use parameters in the functional and to parametrize the method to a given test set. For example, the M06 functional employs a number of 36 parameters determined by a large benchmark study (Zhao and Truhlar, 2008). However, past experience suggests that these methods are mainly suited for systems of marked similarity to the ones included in the fitting sets. Benchmarks from arbitrary molecular systems which are not covered by fittings, such as the “Mindless Benchmark” set (Korth and Grimme, 2009), contribute significantly towards the identification of generally applicable methods. Notice that there exists also the alternative strategy: improving the underlying theoretical framework without introducing empirical parameters. The prominent example of this direction bases on the relatively old PBE functional (Perdew et al., 1996) that has experienced several modifications with a modern functional addressing major drawbacks of DFT (Eshuis and Furche, 2011; Zhang et al., 2012; Adamo and Barone, 1999).
Substantial inherent errors in pure density functional theory include the lack of van der Waals type of interaction that originates from dynamical correlation. Such interactions are conveniently introduced by an atom pair-wise dispersion potential of which the most recent and prominent is Grimme’s D3 correction (Grimme et al., 2011) which requires only minimal additional computational effort. Another description based on the electron density is also available with the VV10 method (Hujo and Grimme, 2011; Vydrov and Van Voorhis, 2010) as -NL extension to existing density functionals, being calculated during the density functional evaluation and of higher computational cost. The inclusion of dispersion interactions has become increasingly important, in particular for the more accurate description of charged molecules or organo-metallic systems, allowing for an appropriate examination of industry-relevant systems such has catalysts or magnetic materials (Grimme et al., 2016). Other DFT approaches like Meta-GGA (M06 (Zhao and Truhlar, 2008), PW6B95 (Zhao and Truhlar, 2005), TPSS0 (Tao et al., 2003)) and range separated functionals (CAM-B3LYP (Yanai et al., 2004), ωPBEh (Rohrdanz et al., 2009), ωB97X (Chai and Head-Gordon, 2008)) lead to an even better description of structural parameters and electronic excited states.
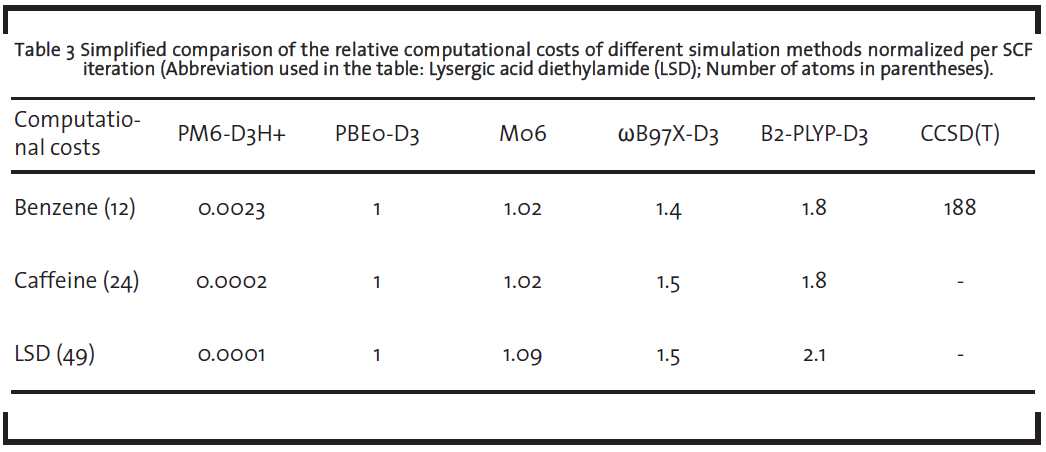
A great leap in the accuracy which exceeds pure DFT functionals was achieved as a result of new methods such as the group of double hybrid functionals. For instance, the prototype B2PLYP-D3 and derivatives (Goerigk and Grimme, 2014) have become state-of-the-art methods for the calculation of very accurate thermodynamic data in an acceptable period of time. Latest developments, such as PWRB95, deliver excellent results which are comparable to the classic double hybrids while requiring lower computational expenses which range between DFT and DH-DFT. Ab initio methods such as CCSD(T) are frequently regarded as standard reference due to their very high accuracy. As a result of simplifications such as DLPNO-CCSD(T), their high computational cost can be significantly reduced (Riplinger and Neese, 2013; Riplinger et al., 2013). A simplified comparison of computational cost of some popular simulations methods is shown in Table 3.

In conclusion, all above, computational materials or synthesis discovery is far from being a black box work-flow including subtle challenges in the application of the appropriate theoretical framework. This complexity requires expertise, experience, and continuous testing and validation of the predictions, all being best-practice in computational materials or syntheses discovery.

3 Conclusion and Outlook

Computational chemistry has become a well-established tool in academic research as well as in industry. The application of quantum mechanics delivers knowledge at the molecular level, particularly on what is happening at specific chemical reaction steps and why certain material properties arise.
Even though there already exists a high number of innovative simulation methods, new simulation methods and potential game-changers are continuously being developed. For instance, if new approaches or significantly more efficient computer technologies can access the world of process scale molecular dynamics (covering realistic timescales of milliseconds to seconds) by accurate methods that rely on none or only few empirical parameters, new insights into temperature and concentration-dependent effects of chemical reactions or materials may become available for additional areas, such as semiconductors, fuel cells and automotive or IoT (Internet of Things) batteries. On the other hand, new methods with a comparable accuracy like DFT and at the cost of semi-empirical methods would also have a massive impact on the size of virtual high throughput screenings and in data generation for innovative machine learning algorithms to develop a specialized artificial intelligence for chemistry.
The modification of chemical systems, the computation of properties, and their analysis can be automated in many areas; current virtual high throughput screening technologies allow improvements of chemical synthesis or of a material to be rapidly identified. This reduces personnel requirements as well as development time and costs significantly, as only the most promising systems need to be analyzed in the laboratory. Consequently, competitors who rely on cheap labour and fewer regulations may lose their competitive advantage because scalable quantum chemical investigations can be done faster, cheaper, and analyse more details. With the help of modern, highly accurate simulation methods, enormous productivity gains, and faster time-to-market can be achieved.
However, this advancement comes with a cost: the high diversity of suitable and unsuitable methods and approaches renders it often virtually impossible for individual professionals to effectively and competently cover this cross-sectional technology (combining quantum mechanics, chemistry, physics, materials science as well as hardware and software technology). Experience shows that only a multidisciplinary and experienced team of chemists, quantum chemists, physicists, and IT specialists is able to produce relevant and realistic simulation data and to process and evaluate it in a very fast way and support the industries R&D specialists with key information at molecular level to develop new game-changing syntheses and materials.

Acknowledgments

We would like to thank Stefan Grimme and Alexander A. Granovsky for fruitful discussions and their helpful advices. We would also like to thank the Humboldt-Innovation GmbH for support.

References

Adamo, C., Barone, V. (1999): Toward reliable density functional methods without adjustable parameters: The PBE0 model, The Journal of Chemical Physics, 110 (13), pp. 6158-6170.

Andersson, M. P., Bligaard, T., Kustov, A., Larsen, K. E., Greeley, J., Johannessen, T., Christensen, C. H., Nørskov, J. K. (2006): Toward computational screening in heterogeneous catalysis: Pareto-optimal methanation catalysts, Journal of Catalysis, 239 (2), pp. 501-506.

Burns, L. A., Vázquez-Mayagoitia, Á., Sumpter, B. G., Sherrill, C. D. (2011): Density-functional approaches to noncovalent interactions: A comparison of dispersion corrections (DFT-D), exchange-hole dipole moment (XDM) theory, and specialized functionals, The Journal of Chemical Physics, 134 (8), pp. 1-25.

Chai, J.-D., Head-Gordon, M. (2008): Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Physical Chemistry Chemical Physics, 10 (44), pp. 6615-6620.

Curtarolo, S., Hart, G. L. W., Nardelli, M. B., Mingo, N., Sanvito, S., Levy, O. (2013): The high-throughput highway to computational materials design, Nature Materials, 12 (3), pp. 191-201.

Eshuis, H., Furche, F. (2011): A parameter-free density functional that works for noncovalent interactions, Journal of Physical Chemistry Letters, 2 (9), pp. 983-989.

Gaus M., Cui Q., Elstner M. (2011): DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB), Journal of Chemical Theory and Computation, 7 (4), pp. 931-948.

German Catalysis Society (2010): Roadmap for Catalysis Research in Germany: Catalysis – A key technology for sustainable economic growth, Dechema, Frankfurt.

Goerigk, L., Grimme, S. (2014): Double-hybrid density functionals, Wiley Interdisciplinary Reviews: Computational Molecular Science, 4 (6), pp. 576-600.

Greeley, J., Jaramillo, T. F., Bonde, J., Chorkendorff, I., Nørskov, J. K. (2006): Computational high-throughput screening of electrocatalytic materials for hydrogen evolution, Nature Materials, 5, pp. 909-913.

Grimme, S. (2014): A general quantum mechanically derived force field (QMDFF) for molecules and condensed phase simulations, Journal of Chemical Theory and Computation, 10 (10), pp. 4497-4514.

Grimme, S., Antony, J., Ehrlich, S. and Krieg, H. (2010): A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, The Journal of Chemical Physics, 132 (15), pp. 1-19.

Grimme, S., Ehrlich, S., Goerigk, L. (2011): Effect of the damping function in dispersion corrected density functional theory, Journal of Computational Chemistry, 32 (7), pp. 1456-1465.

Hujo, W., Grimme, S. (2011): Performance of the van der waals density functional VV10 and (hybrid)GGA variants for thermochemistry and non-covalent interactions, Journal of Chemical Theory and Computation, 7 (12), pp. 3866-3871.

Jain, A., Hautier, G., Moore, C.J., Ping Ong, S., Fischer, C. C., Mueller, T., Persson, K. A., Ceder, G. (2011): A high-throughput infrastructure for density functional theory calculations, Computational Materials Science, 50 (8), pp. 2295-2310.

Kamerlin, S. C. L., Warshel, A. (2011): The empirical valence bond model: Theory and applications, Wiley Interdisciplinary Reviews: Computational Molecular Science, 1 (1), pp. 30-45.

Korth, M., Grimme, S. (2009): Mindless DFT benchmarking, Journal of Chemical Theory and Computation, 5 (4), pp. 993-1003.

Koskinen, P., Mäkinen, V. (2009): Density-functional tight-binding for beginners, Computational Materials Science, 47 (1), pp. 237-253.

Kromann, J. C., Christensen, A. S., Steinmann, C., Korth, M., Jensen, J. H. (2014): A third-generation dispersion and third generation hydrogen bonding corrected PM6 method: PM6-D3H+, PeerJ, pp. 1-18.

Kruse, H., Goerigk, L., Grimme, S. (2012): Why the standard B3LYP/6-31G* model chemistry should not be used in DFT calculations of molecular thermochemistry: Understanding and correcting the problem, Journal of Organic Chemistry, 77 (23), pp. 10824-10834.

Mackerell, A. D. (2004): Empirical force fields for biological macromolecules: Overview and issues, Journal of Computational Chemistry, 25 (13), pp.1584-1604.

Maier, W. F., Stowe, K., Sieg, S. (2007): Combinatorial and high-throughput materials science, Angewandte Chemie: International Edition, 46 (32), pp. 6016-6067.

Perdew, J., Burke, K., Ernzerhof, M. (1996): Generalized Gradient Approximation Made Simple, Physical review letters, 77 (18), pp. 3865-3868.

Riplinger, C., Neese, F. (2013): An efficient and near linear scaling pair natural orbital based local coupled cluster method, Journal of Chemical Physics, 138 (3), pp. 1-18.

Riplinger, C., Sandhoefer, B., Hansen, A., Neese, F. (2013): Natural triple excitations in local coupled cluster calculations with pair natural orbitals, Journal of Chemical Physics, 139 (13), pp. 1-13.

Rohrdanz, M. A., Martins, K. M., Herbert, J. M. (2009): A long-range-corrected density functional that performs well for both ground-state properties and time-dependent density functional theory excitation energies, including charge-transfer excited states, Journal of Chemical Physics, 130 (5), pp. 1-8.

Stewart J. J. P. (2007): Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements, Journal of Molecular Modeling, 13, pp. 1173-1213.

Stewart, J. J. P. (2013): Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters, Journal of Molecular Modeling, 19 (1), pp. 1-32.

Sure, R., Grimme, S. (2015): Comprehensive Bench mark of Association (Free) Energies of Realistic Host Guest Complexes, Journal of Chemical Theory and Computation, 11 (8), pp. 3785-3801.

Tao, J., Perdew, J. P., Staroverov, V. N., Scuseria, G. E. (2003): Climbing the Density Functional Ladder: Non-Empirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Physical Review Letters, 91 (14), pp. 1-4.

Van Duin, A. C. T., Dasgupta, S., Lorant, F., Goddard, W. A. (2001): ReaxFF: A reactive force field for hydrocarbons, Journal of Physical Chemistry A, 105 (41), pp. 9396-9409.

Vydrov, O. A., Van Voorhis, T. (2010): Nonlocal van der Waals density functional: The simpler the better, Journal of Chemical Physics, 133 (24), pp. 1-9.

Yanai, T., Tew, D. P., Handy, N. C. (2004): A new  hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chemical Physics Letters, 393 (1-3), pp. 51-57.

Zhang, I. Y., Su, N. Q., Brémond, É. A. G., Adamo, C., Xu, X. (2012): Doubly hybrid density functional xDH-PBE0 from a parameter-free global hybrid model PBE0, Journal of Chemical Physics, 136 (17), p. 1-8.

Zhao, G., Perilla, J. R., Yufenyuy, E. L., Meng, X., Chen, B., Ning, J., Ahn, J., Gronenborn, A. M., Schulten, K., Aiken, C., Zhang, P. (2013): Mature HIV-1 capsid structure by cryo-electron microscopy and all atom molecular dynamics, Nature, 497 (7451), pp. 643-646.

Zhao, Y., Truhlar, D. G. (2005): Design of density functionals that are broadly accurate for thermochemistry, thermochemical kinetics, and nonbonded interactions, Journal of Physical Chemistry A, 109 (25), pp. 5656-5667.

Zhao, Y., Truhlar, D. G. (2008): The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theoretical Chemistry Accounts, 120 (1), pp. 215-241.