When data science meets patent information – Analyzing complex business environments of innovation-driven industries
Abstract
The rapid development of the internet as well as the emergence of new technologies such as smart devices leads to an exponential growth of data that hold useful information for companies. To face this trend new methods were developed, which allow to analyze large amounts of data in short time. This enables to investigate topics in a broader context, what again offers interesting new insights. Among the different data types that can be analyzed, especially patents represent an important information source for companies that hold unique technological information. Therefore, analyzing patents can reveal research, technology, and innovation activities in industries, which enhance a company’s decision making in relation to its R&D activities by better understanding its complex environment. This makes the patent analysis an indispensable task for companies. In this article, we aim to show case the ease and value of data-driven patent analysis. Already simple methods such as counting or connecting single patent information reveal through different visualization various insights in a business environment and improve its understanding. Towards this goal, we provide four case studies based on patents stemming from the fields of stem cells, lithium-based batteries, antibiotics, and personalized medicine. Thereby, each case features different data mining techniques to present readers a broad range of application examples.
1 Introduction
The rapid networking of the modern world caused a widely spread of knowledge and technologies, which consequently led to an increasing rate of change due to shorter product life cycles (Qualls et al., 1981), increasing technological changes (Sood and Tellis, 2005), increasing innovation speed (Parry et al., 2009) and an increasing speed of the diffusion of innovations (Lee et al., 2003). Due to these developments, the world is characterized by growing environmental changes and complexity, which must be considered in a company’s strategy. On the one hand, results a growing necessity to create innovations to survive in an environment that is characterized by pervasive, unpredictable, and continuous changes (Aydogan, 2009). On the other hand, the growing complexity hampers the innovation capabilities of companies because it requires the observation of the whole environment for changes to overcome the uncertainty of the company and be able to respond to changes in time (Day and Schoemaker, 2004). However, the understanding of the environment requires the gathering and analysis of external data sources. Through the rapid development of the internet in combination with the emergence of new devices, such as smart phones, the amount of data grows exponentially. Estimations in 2015 presented that roughly 90% of the data all over the world was created in the two preceding years due to the emergence of new devices, sensors, and technologies (Kroker, 2015). While the opportunities to analyze and use external data for the own strategic purpose grow, the investigation of the growing amount of information becomes an increasingly harder task that results in an enormous expenditure on desk research and exceeds the capacities of companies. Hence, to face the so called data explosion and fully exploit its potential new analysis methods were needed. For this purpose, the field of data science emerged that aims to extract knowledge from great amounts of data.
Data science is a field that developed due to advances in hardware and software technology over the years. It focuses on processing high quantities of data through the development of algorithms or respectively statistical methods to find hidden patterns in large datasets. Data science methods extends the manual analysis by enabling not only to analyze single parameters but to analyze combinations of parameters, whereby hidden connections with higher strategic significance, in comparison to isolated key figures, can be revealed (Ernst, 2003; Siwczyk, 2010). Therefore, data science methods changed the way we can analyze data, what enables companies to get a broader and deeper look on data. In return companies can exploit data sources to better understand their environment, which enhance their decision making. It results that these methods became indispensable for companies to gain unique knowledge from data that could lead to competitive advantages. Noteworthy is that the developments of the internet and new devices not only caused growing amounts of data but also promotes a greater variety. Depending on what type of data is analyzed different information about the environment can be investigated. For instance, scientific publications mostly hold information about basic and applied research while social networks may rather represent social opinions (Kayser, 2016). Among the variety of data types, especially patents represent a source with unique information, whose analysis with data science methods can create great benefits for companies.
Patents are a primary data source for technological information that are well suited to be analyzed by data science methods. What distinguishes patents from other information sources is that 80 per cent of their content is not available anywhere else (Dou, 2005). Furthermore, a higher level of detail and range of information results in a more comprehensive information source in comparison to other sources such as scientific publications (Bonino et al., 2010). Generally, patents are used for legal protection of innovations, which has especially in innovation-driven industries great importance (Reitzig 2004; Smith and Hansen, 2002). They can strengthen a company’s competitive standing by systematically limiting the scope of action of competitors (Hentschel, 2007). Moreover, they can open up access to complementary patents of competitors through the usage of patents as a kind of currency in cross-licensing agreements (Hentschel, 2007). It also play an important role in the case of decision making relating to cooperation partners as well as merger and acquisition, because a well-positioned and balanced patent portfolio represents an important strategic factor. Consequently, analyzing patent data enables to grasp research, technology, and innovation activities in industries, wherefore patents can be used as an indicator for the creation of knowledge as well as for empiric innovation research. Therefore, combining patents and data science methods can offer huge potential for understanding business environments and trends, which enhances decision making.
With this paper we want to provide readers with an initial understanding of the application of data science methodologies on patents. Therefore, we present 4 case studies taken from highly relevant technological fields. These cases are only analyzed with simple data science methods that deal with counting certain information like application numbers or linking information like frequencies of patent applications with patent applicants. By considering different information in the patent data and using methods to visualize the results in different ways, the variety of insights in the industries that can be grasped by these methods will be presented. Concluding, the execution of these cases is also intended to give the readers insights how patent analysis through simple data science methods can be a contribution to understand business environments. The remainder is of this paper is organized as follows: Section 2 briefly describes the theoretical background for the research setting. Section 3 presents the four case studies including the analyses steps and their results. At last, section 4 summarizes the major findings followed by a conclusion and limitations in section 5.
2 Theoretical Background
2.1 Data Science
The growing amount of available data attract the attention of many industries, which realized great potential to achieve competitive advantages through its analysis. Although, companies possess teams of statisticians and modelers that can exploit datasets, the vast amount of data exceeds the possibility for manual analyses by far. Meanwhile, strong improvements in hardware lead to far more powerful computers, which allow to develop algorithms that analyze connections between multiple datasets to get a deeper and broader insight into data. The convergence of both developments resulted in the emergence of the data science field. Data science includes principles, processes, and techniques to (automatically) extract knowledge from data. Therefore, an understanding for new phenomena or respectively the company’s environment based on data can be built that enhances decision making. Here, the resulting data-driven-decision-making does not completely replace previous procedures for decision making but supports decisions that based purely on intuition before. The effect of this procedure on firm performance was measured by Brynjolfsson, Hitt & Kim (2011), who showed a positive correlation between the application of data based decision making and the profitability of a company. For this reason, more and more companies from different industries started to apply data science methods to improve their business. Depending on the industry, different techniques and types of data are needed. So, delivery services like UPS uses data science algorithms to analyze traffic data from their employees in combination with further data information such as weather or logistics data to optimize its package transport from drop-off to delivery (Samuels, 2017). The health care sector uses data science methods among other things in cancer care. To offer patients personalized chemotherapy and radiation regimens data of cancer patients from the past years in form of diagnoses, treatment plans, outcomes and side effects is analyzed to derive personalized recommendations for future cancer patients (Rice, 2019). Quite different, companies who focus on the online market such as Google or respectively E-Commerce like diverse retailers analyze the data profiles of the internet users (Rice, 2019). Therefore, behavioral patterns can be derived, which enable to create customized layouts and spotlighted products. Also, the price of products can be personalized depending on the users profile, from which his willingness to pay can be derived. In conclusion, depending on the industry different sorts of data and therefore different insights can be important for the business. When we take a look at innovation-driven industries, such as the pharmaceutical industry, especially patent data play an important role (Reitzig 2004; Smith and Hansen, 2002), because creating and patenting innovations involve high costs and efforts. While in many other industries data can be used to optimize the business, innovation-driven industries are strongly dependent on patents due to their strong influence on the performance of the business. Therefore, patents for such industries contain extensive and vital information about their environment. For this reason, patent data and its relevance are the focus of this paper.
2.2 Patents and their relevance
Patent law is a worldwide accepted and established process to protect innovative products or processes, which has gained great importance especially in innovation-driven industries This is represented through the numbers of patent applications, which has been rising since 1990. In 2018 already the German patent office Deutsches Patent- und Markenamt (DPMA) received over 67.000 patent applications (DPMA, 2018) and the worldwide patent application grew by five per cent in the same year compared to the previous year (WIPO, 2019). Patents represent a unique form of publications because their acceptance depends on general legal conditions. These take into consideration that inventions to be patented have to fulfill the following requirements being a novel invention, inventive activity must be present and industrial applicability must be possible. Also, the invention with a detailed description must be made public, what does not guarantee that the invention will be patented and could be a risk for the inventor. Only when all these conditions are fulfilled, the patent with its legal protection can be granted. Therefore, patents differentiate themselves from other publications such as scientific journals or books, because the grant of a patent is associated with greater hurdles. For this reason, patents are a more reliable source in comparison to other sources.
Patents represent further an information source with various advantageous properties for analyses, which Dreßler (2006) had summarized. Firstly, the patent applicant is obligated to reveal all technical details of the invention that is to protect. Therefore, patent information is freely available in the public database of the responsible patent office for every user group. Additionally, through the progress of the digitalization of information, a quick access and research via internet is favored. Moreover, the information is revealed before the market launch, which enables among other things an analysis of the technological state of the art. From this can be concluded that patents are suitable for representing the most recent trajectory of technologies to predict future trends, which makes them indicators for early trend detection due to its high actuality. The neutral audit process through public authorities leads further to an objective assessment and due to the implementation of a uniform classification system patents are standardized. Another requirement on patents is that they have to be understandable described to make the invention and its value comprehensible for everyone. The introduction of a patent classification system, such as the international patent classification called IPC, enables to precisely describe a technology and to classify patents into technology classes. This makes patents more comparable and enhances the search for certain technology fields. At last, with the application of a patent the commercial value must be given. This means, that accepted patents represent technologies with potential for commercial usage. Consequently, analyzing patent data with data science methods in terms of patent management can offer important technical, business, and legal insights (Park et al., 2013), which in sum supports companies to understand the big picture.
2.3 Patent structure and information
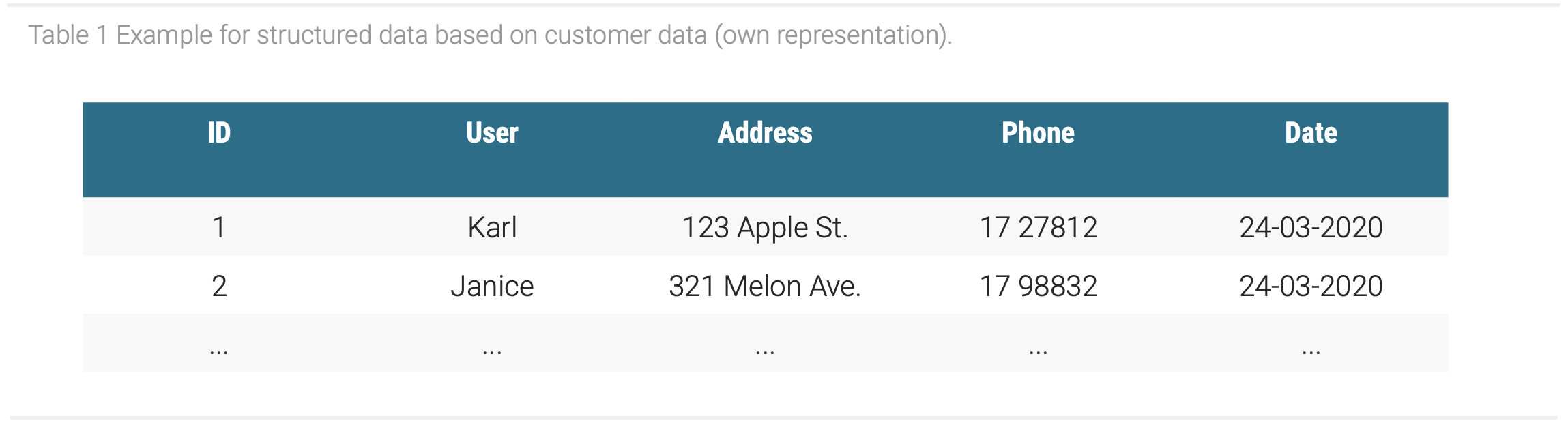
The structure of patents consists of bibliographic and technical data of an invention. The structure can also be divided into a structured and unstructured part. Data in general can possess a structured, semi-structured or unstructured form (Tanwar et al., 2015). This leads to a structural heterogeneity, while only a small part of all data is structured (Cukier, 2010). Structured data is represented through tabular data and is managed with relational data-bases and spreadsheets. Each data point possesses a clear relation to the others, which enables to store them with traditional row-column databases such as SQL. Structured data is further characterized by being highly organized and easily machine-processable. The management of the data with relational databases enables a user to quickly input, search, and manipulate structured data (Din, 1994). The Table 1 shows an example for structured data, where each information of a customer can be easily stored in the relational database because of the relation of each information to a column. Moreover, the data can be directly analyzed, for example on which date the most customers were recorded, without the need for any further steps.
In contrast, data without format, schema, or structure is referred to as unstructured data. It can possess any form such as texts, videos, images, or PDFs. While structured data can be easily processed by machines, the processing and analysis of unstructured data by machines is complicated (Allahyari et al. 2017). An example for unstructured data is the following sentence.
“The customer Carl has made a transaction on the 24th of March 2020.”
The form of this data type hinders the storage of the data into a relational database. As a result, the implementation of analysis steps requires preprocessing steps to enable the storage of information from the text into a relational database. In other words, the unstructured text has to be first converted into a structured format to obtain a machine-readable form and be able to gain insights from the data.
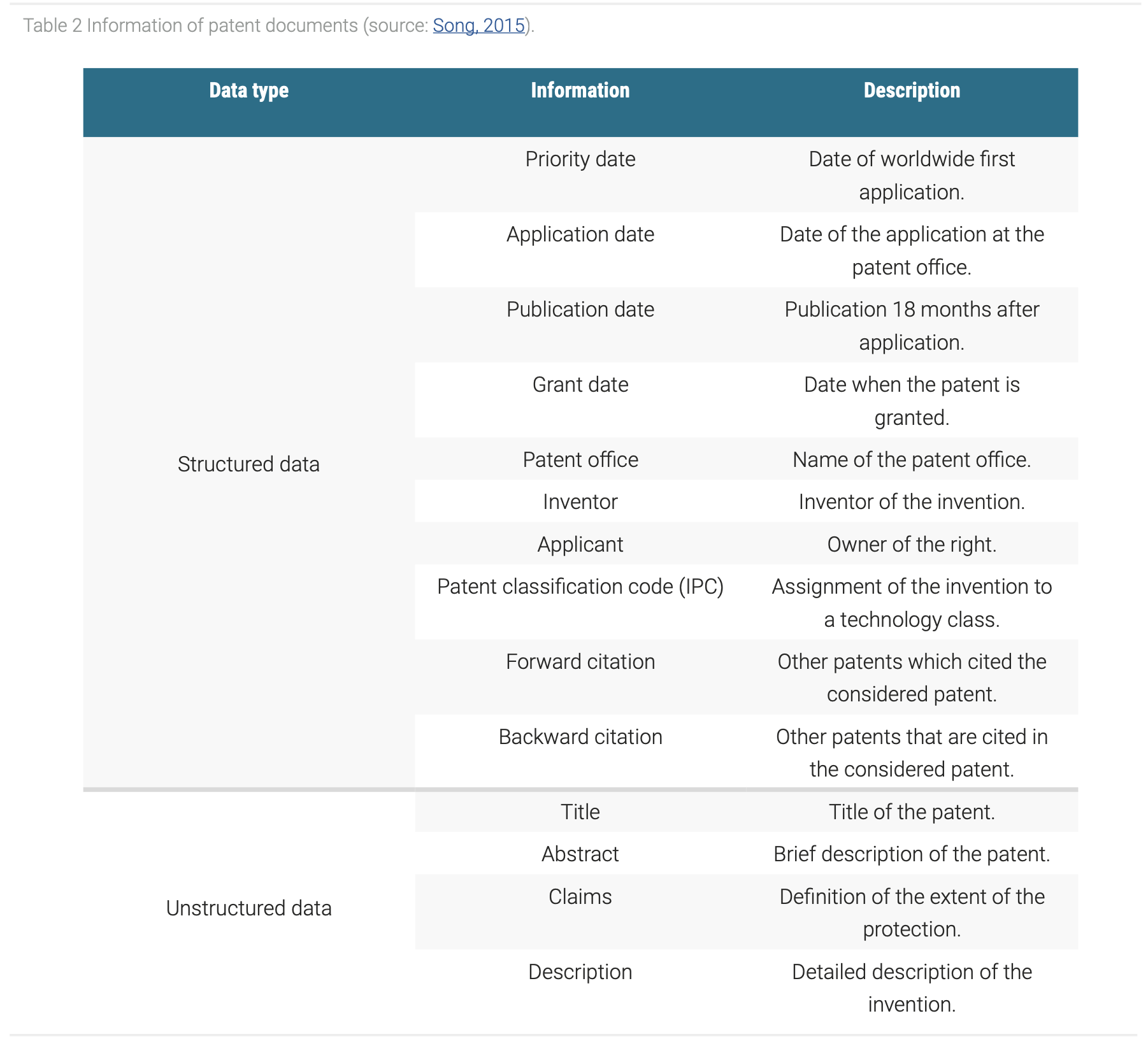
Patents possess a semi-structured format. Table 2 shows that most of patent information is structured, such as the IPC codes, and can be directly used for analyses. The structured part of patents includes bibliographic data, which represents information about formalities such as the inventor, application date or technology classification through IPC. The unstructured part is represented through descriptive texts such as the abstract or claims. Although, the text data in patents can be assigned to title, abstract, claims and description, the information is unstructured in themselves. Therefore, specific data science methods must be applied first to analyze these parts of patents.
The broad range of information allows to analyze many different aspects of an invention. For example, from the assignment of patents to its applicant, important strategic information about the competitive environment can be derived. This includes the identification of growing danger potential from competitive companies but also the estimation of the freedom to operate in the own R&D efforts to act with foresight and prevent unnecessary spending of resources. Moreover, different aspects can put into context to find correlations or hidden patterns in the patent landscape. For instance, the analysis of the number of applications in a certain technology area over the years can reveal how the research effort in general has developed, which enable to draw conclusions about the future potential of this research field. However, when the number of application is analyzed in relation to the applicants it may reveal a ranking with the most active players in that field. Therefore, further implications can be drawn such as strongly represented countries or the most represented types of applicants. The text passages on the other hand hold potential for analyzing buzz words, to find for example new emerging topics in the targeted technology area. It results, that patents offer many aspects to analyze on its own, but also enable to consider multiple aspects in one context, which extends the possibilities to draw valuable insights into industries.
In each of the four following cases, different data science methods are applied. These are simple methods for counting individual pieces of information or for linking them. Following, various visualization techniques are used to present the results. This includes besides classic representations such as histograms or bar charts, network analysis that not only enable to show the frequency of individual elements, but also the link between elements in the form of nodes and edges. Therefore, the relationship between specific elements can be investigated. Through the usage of different methods and patent information in each case, various insights are generated that enable to understand a unique part of the business environment. Since the analysis of unstructured data requires a deeper insight into the subject area of data science, the following cases are mainly focused on the analysis of the structured parts of the patents.
3 Case studies
3.1 Tracing research efforts in the field of antibiotics
Alexander Fleming’s discovery of penicillin in 1928 is one of the most prestigious milestones in the history of medicine – or even modern science. Based on his initial discovery, the development and industrial production of penicillin-related antibiotics enabled the efficient treatment of bacterial infections, which, at that time, would often lead to death (e.g. through sepsis) (Mutschler et al., 2001). Even though Fleming conducted his experiments almost a century ago, the treatment of bacterial infections still remains a current challenge due to the rise of antibiotic resistance in certain bacteria. Solely in the European Union, infections caused by antibiotic resistant bacteria amount to approximately 33,000 deaths per year. Nevertheless, the annual number of new broad-spectrum antibiotics has been continuously decreasing, and more and more pharmaceutical companies have announced that they are going to stop, or have already stopped, their research on antibiotics (NDR, 2019). The result is a market failure of serious consequence.
Against this background, we set our first case study and aim to trace the research efforts for β-lactam antibiotics – the biggest group of broad-spectrum antibiotics – in recent years. Thereby, we want to focus on two specific aspects:
- How has the research efforts for β-lactam antibiotics developed?
- Who are/were the active actors in this field?
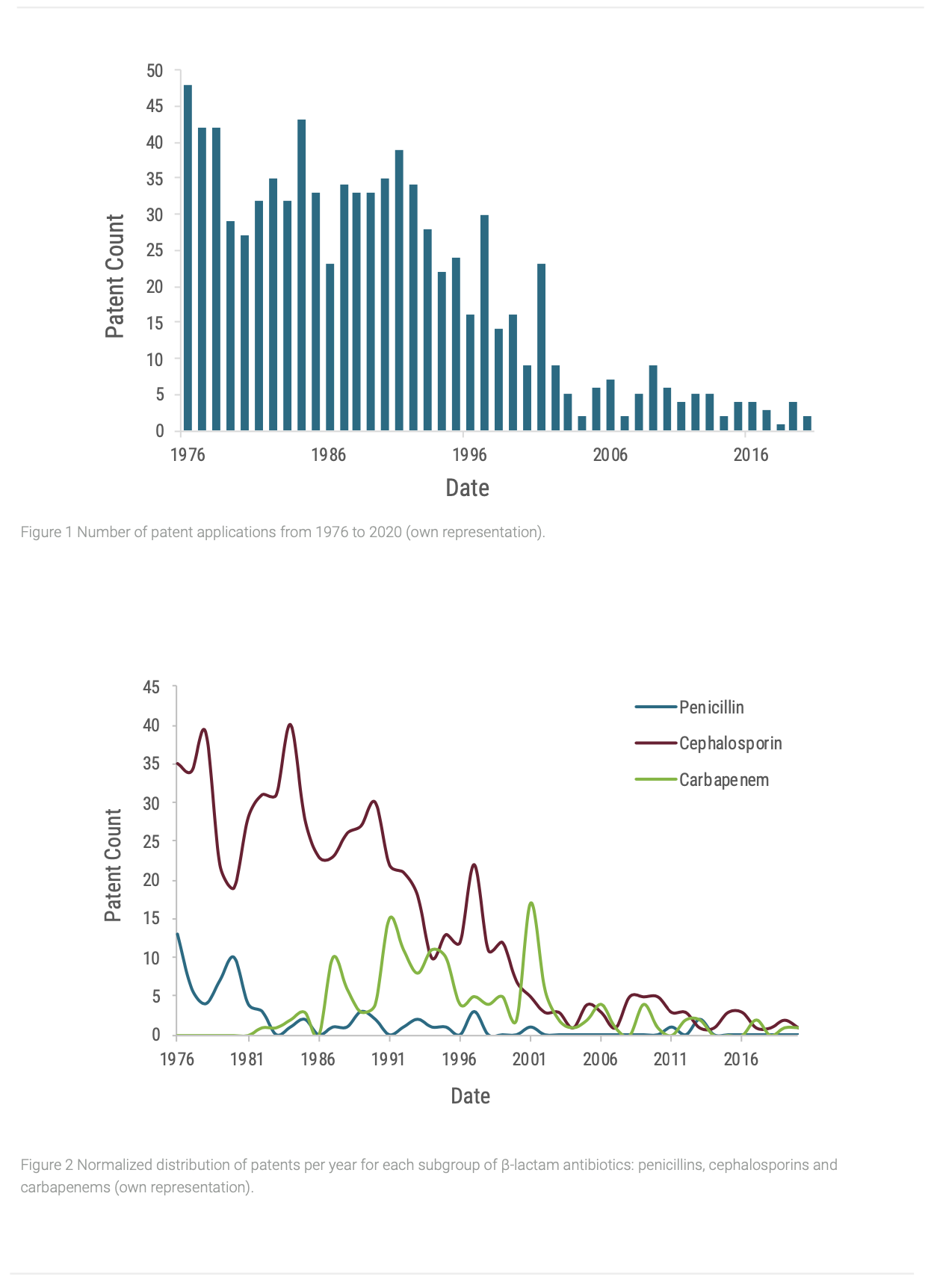
To answer these questions, we used simple visualization techniques on a dataset of 872 patents, which were extracted from PatentsView, a platform that provides data from the US Patent and Trademark office. By plotting the number of submitted patent applications throughout the years, the severity of the research reduction becomes immediately evident (Figure 1). While the late 1980s and early 1990s are marked by constant patent applications in the field of antibiotics, the number of patent applications register a steep drop after 1993. This development indicates that research for new β-lactam antibiotics have become unprofitable for major pharmaceutical companies in the mid to late 1990s (Katz et al., 2006). To further investigate this assumption, it is worth to differentiate between the most important subgroups of β-lactam antibiotics, namely: penicillins, cephalosporins and carbapenems. In our dataset, 74% of all granted patents were for cephalosporins. This circumstance is reasonable according to the structural flexibility of this chemical compound. Because of distinct development stages, the time-dependent distributions are very different (Figure 2). Whereas the decline in patent applications for penicillins commenced very steeply in the 1980s, the decline for cephalosporins was more gradual. The application rate for patents concerning carbapenems-based antibiotics, on the other hand, increased until the early 1990s and only then decreased again. These courses can be understood by the different developmental stages of the antibiotic classes. The first carbapenem antibiotics were developed in the 1980s by researchers at Merck & Co, while penicillins and cephalosporins became widely researched antibiotics as early as the end of World War II (Birnbaum et al., 1985). Nonetheless, they all converge to very low rates at least since the 2000s.
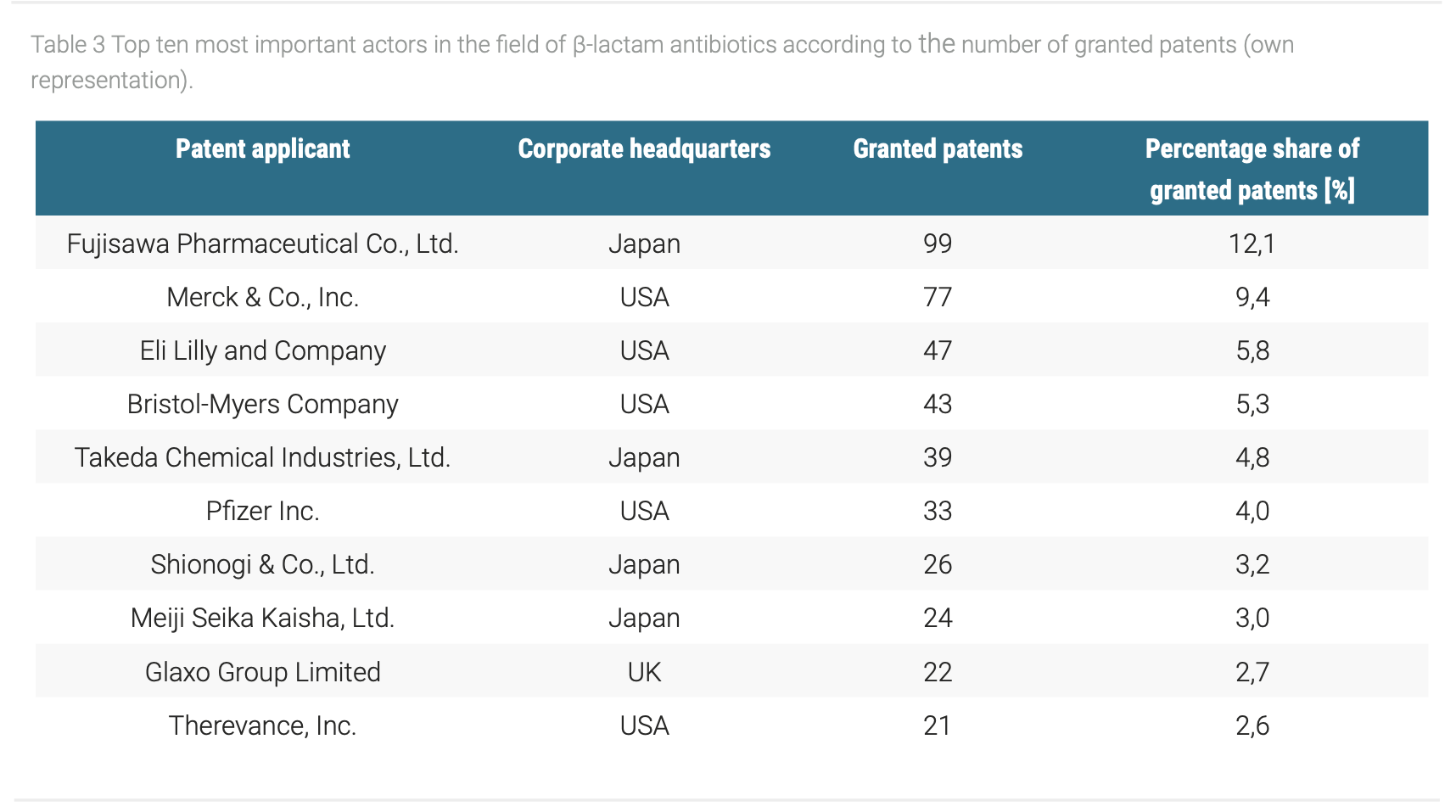
Now that we have unraveled the strong decline in research efforts concerning β-lactam antibiotics, it is worth to investigate who the actors were that developed new β-lactam antibiotics. For this purpose, we shift our focus to the patent applicants. By simply counting the number of applied patents per applicant, we can gain a good overview on the actors in this field. An excerpt of the most active applicants is given in Table 3 – interestingly, these are almost entirely of Japanese or American origin. Apart from the strong geographical dominance, there is a clear lack of universities as all of the most important actors were firms. This emphasizes the strong market and application driven focus of the research efforts in the field of β-lactam antibiotics.
Strikingly, these ten companies alone are responsible for 53% of all patents. Thereby, Fujisawa Pharmaceutical Co. and Merck & Co. have solely contributed a fifth of all β-lactam antibiotics patents. The strong decline in patent applications, however, cannot be explained by the discontinuation of research efforts of a singular firm but indicates rather a systemic development affecting most, if not all of these pharmaceutical companies. According to the analyzed patent data, β-lactam antibiotics seem to be obsolete. This finding may underline the opinion of experts who propagate new approaches beyond antibiotics (Hancock, 1997). Furthermore, so-called blockbuster drugs (e.g. anti-cancer drugs) hold the promise to generate much more revenue compared to medication for short-time therapy.
Taken together, in this case, we were able to shed light onto past research efforts in the field of β-lactam antibiotics. Using simple visualization techniques, we could demonstrate that research efforts in this area been declining. Furthermore, we could easily identify the most important actors. By using these easy to use steps, we were able to quickly familiarize our self with the field of β-lactam antibiotics and find evidence for the decline in research activities. The brilliant thing about data science is that once we have programmed these steps, we can easily apply them to new data sets to explore new topics. To prove this point, we use the next case to explore the field of personalized medicine.
3.2 Learning about personalized medicine
To contrast the first case, in the second case we will use similar steps to familiarize ourselves with the field of personalized medicine, starting with a short explanation. Personalized medicine (PM) is an advancing technology with major potential for multiple medical fields like oncology, auto-immunology and even psychiatry (Chan and Ginsburg, 2011; Davis et al., 2009). It is based on individuals’ genetic and genomic information, which allows patient stratification, resulting in tailored preventive and therapeutic measurements (Green and Guyer, 2011). Hence, PM offers various application opportunities – from preclinical diagnosis, over pharmacogenomics, to molecular-targeted therapies. To foster the advantages of PM for modern health care, findings from basic research about the human genome have to be utilized and innovative products have to be developed, like diagnosis devices for disease-related biomarkers or anti-body-directed therapeutics (Chan and Ginsburg, 2011). Consequentially, PM may revolutionize the field of medicine in a similar way to Fleming’s discovery of antibiotics. However, from this hypothesis interesting questions arise:
- At which maturity stage does the technology stand right now?
- Who is driving the research in the field of personalized medicine?
To receive a broad overview about the technology, patent titles and abstracts were searched with the general query terms “personalized medicine”, “patent stratification” and “targeted therapy”, rather than focusing on specialized technology within the field of PM, which may distort the results. Based on these search queries, we were able to download 589 PM patents from PatentsView. Using programmed scripts to extract specific patent indices from the data set, enables us to use quantitative approaches to trace the progression of the technology life cycle (TLC). As TLC assessment is especially important to guide strategic decision making and investments, data driven methods are useful tools to make technology’s progression observable (Lee et al., 2016). There are further advantages in assessing the TLC by patent application data, because these information are accessible before product lifecycle data occur (Haupt et al., 2007). Though a single patent indicator may not provide full information about the progression of a technology, only the patent application numbers over time is showcased in this case for exemplification.
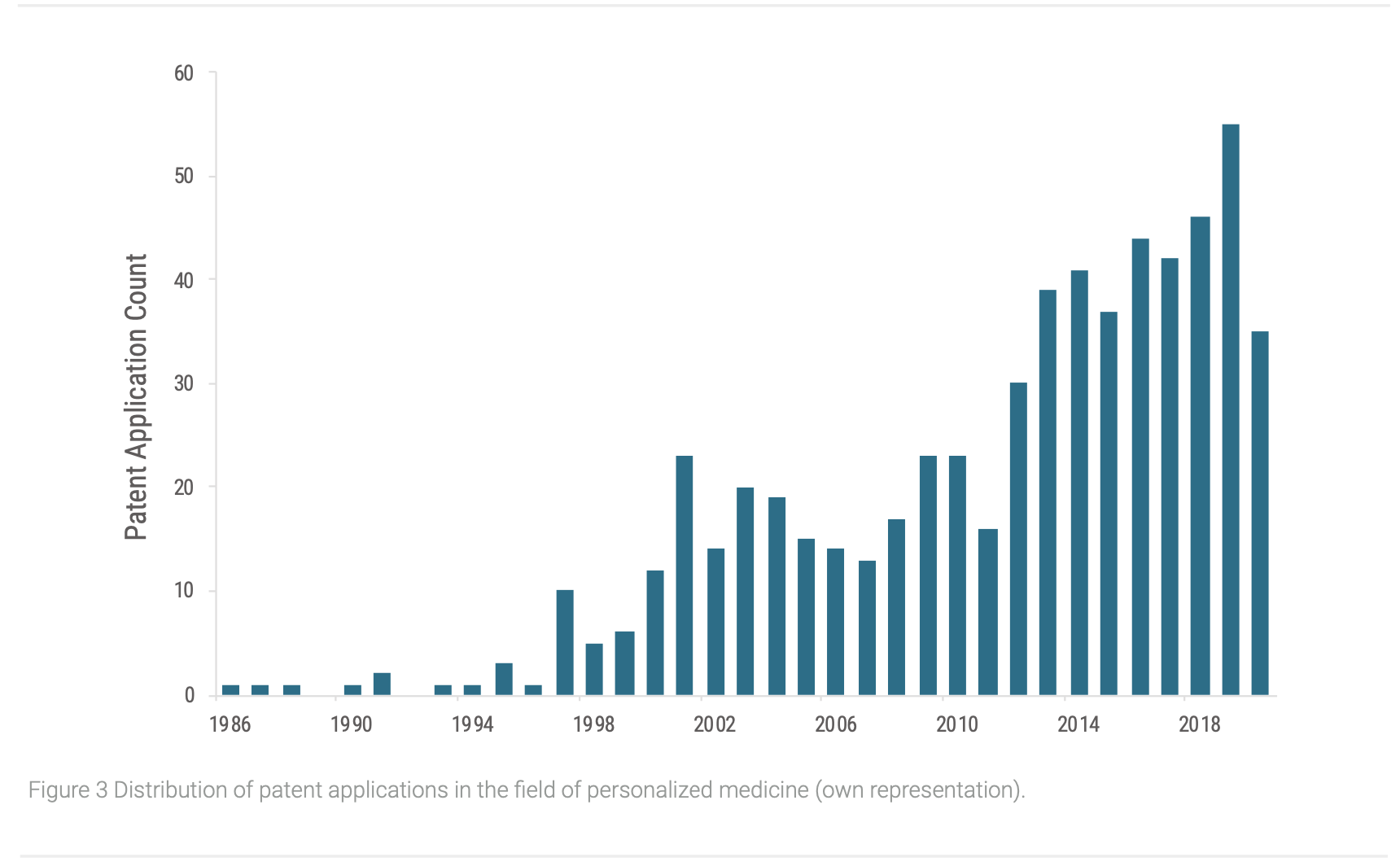
The overall annual distribution of patent applications shows a continually rise of new patents after the turn of the millennial (Figure 3). Especially the decryption of the human genome in 2002 by the Human Genome Project was a major milestone for the development of PM, because it offered deep insights to understand and identify important endogen factors of human health and their diversity. Based on this knowledge, further inventions and applications are developed, which result in increasing numbers of patents in this field (Song et al. 2017; Chan and Ginsburg 2011). Because the annual numbers of patent applications still increase, PM has not reached the maturity stage yet, as after that, patent applications start to decrease (Lee et al. 2016). However, especially in 2006 and 2011 the trend caves in. Essential for this development are more restrictive patent regulations for genetic engineering, because genomic information is broadly classified as “natural phenomena”. Therefore, related inventions are more difficult to receive a granted patent status and even some already granted patents lost their protection status (Chan and Ginsburg 2011; Holman 2015). This might lead to more reserved development of PM by the industry and might slow the overall progress and maturity, as it was observed that the strength of patent protection historically had an impact on the development of the pharmaceutical industry of different nationalities (Achilladelis und Antonakis 2001).
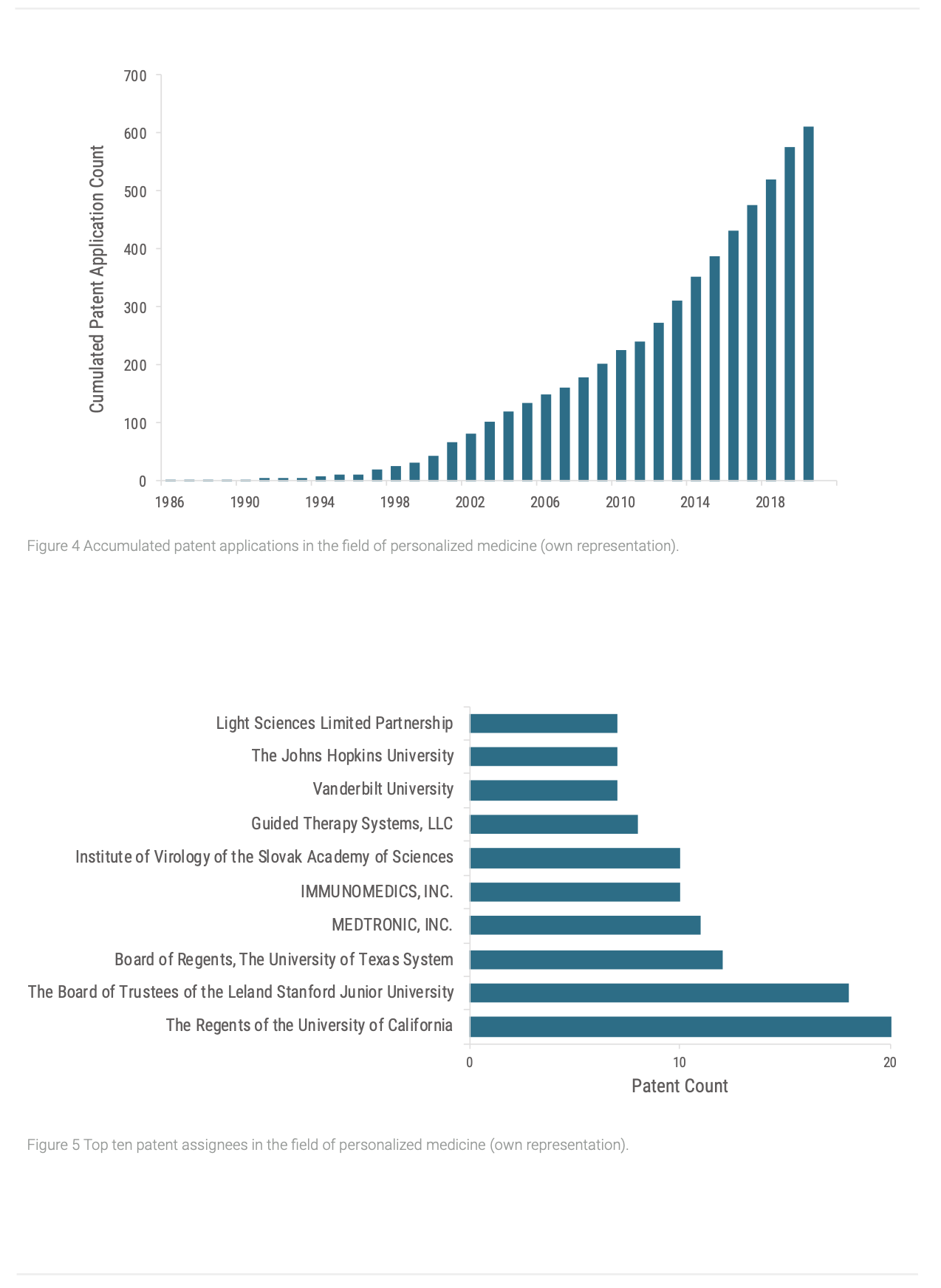
To attain further insights of PM’s current TLC stage, the cumulated patent applications were plotted over time as well (Figure 4). Like the TLC, cumulated patent applications follow an S-shape curve as well, with slowly increasing patent application numbers of basic innovations at the introduction stage, followed by more rapidly increases when the growth stage is arrived, and later patent applications decline when reached maturity (Haupt et al. 2007). Comparably to the annual application numbers, the cumulated ones rise. At the beginning, the trend increases relatively slow which seem to turn around the year 2012, and a more rapid growth is observed. Therefore, PM seems to have reached the early growth stage. Consequentially, we can expect an increasing amount of innovations stemming from the area of PM to penetrate the market in near future.
To gain a deeper understanding of active actors in PM research, we analyzed the individual patent assignees and their number of patent applications. A more detailed look at the assignee organizations revealed that six applicants from the top ten are from academia (Figure 5). Particularly in the US, universities increasingly rely on financing from non-governmental sources to fund their research, like contracts with companies from the industry or spin-offs (Mohrman et al. 2008). Especially new and promising findings from basic research result in rising investments from the pharmaceutical industry into external knowledge (Toole, 2007). So, patents offer opportunities for universities to acquire funding. After a period of waiting and observation of developments from academical research, pharmaceutical companies invest again – this time into internal R&D (Toole 2007). The combination of organizations from academia and industry represented in holding most of the patents leads to the interpretation that the field of PM shifts from basic to more advanced technologies and gains momentum on the market, which supports the previous findings regarding patent activities (Chan and Ginsburg 2011; Haupt et al. 2007).
In conclusion, the technology of PM seems to be evolved from the first stage of introduction to early levels of growth. This might support managerial decisions to start scoping specialized fields of PM for early adoption and differentiation. However, since the technology yet seems to be transitioning between the stages, more patent indices for TLC assessment should be explored for a more detailed observation, so e.g. investment decisions like make- or buy-strategies are able to be made more solidly.
Similar to the first case, this case showed that we were able to gain insights into the current state of the technology life cycle within the field of personalized medicine using relatively simple data analysis measures. While these insights can already provide valuable information about specific technology fields or research topics, more advanced visualization and data science techniques enable us to gain much more detailed and decision-supporting insights – which we will explore a bit more in our next application case.
3.3 Dissecting innovations in the field of lithium-based batteries
For our third case, we leave the realm of medicine and focus on another transforming technology field: energy storage. The path towards a renewable and electric future is marked with many technological barriers. Developing modern battery-technologies plays a key role for future energy infrastructure. Batteries are used in stationary applications like the storage of solar or wind power, as well as in mobile applications, like portable electronics or electric cars. Especially the electrification of mobility is a strong driver for the development of new and powerful battery technologies and will lead to a sharp increase of their demand (Thielemann et al., 2018). Therefore, batteries represent a lucrative future market, however, it is a market with a lot of competition. Moreover, the battery market is very complex, because of the various applications and types of batteries. As a result, various globally distributed companies stemming from different branches are part of the market. Especially in complex technology markets, like the battery-market, a comprehensive patent-analysis can provide important and beneficial knowledge, for example about the competitive landscape. Implemented as a powerful addition to other market analysis techniques it can portray technology trends, reveal market niches, and give insights about the technological strength of competitors. Here we focus on the questions:
- How is the battery market divided and which applicants hold the most patents in the areas?
- What elements gained importance over time?
We focused our search on lithium-based batteries, because they are currently and in prospects the most promising battery-technologies (Scrosati and Garche, 2010). In the following two analyses are presented exemplary, to demonstrate the utility of patent data for a competitive market and technology analysis. In one analysis, using a title-word-search, we investigated the distribution of patent applicants on the battery main components (Figure 6).
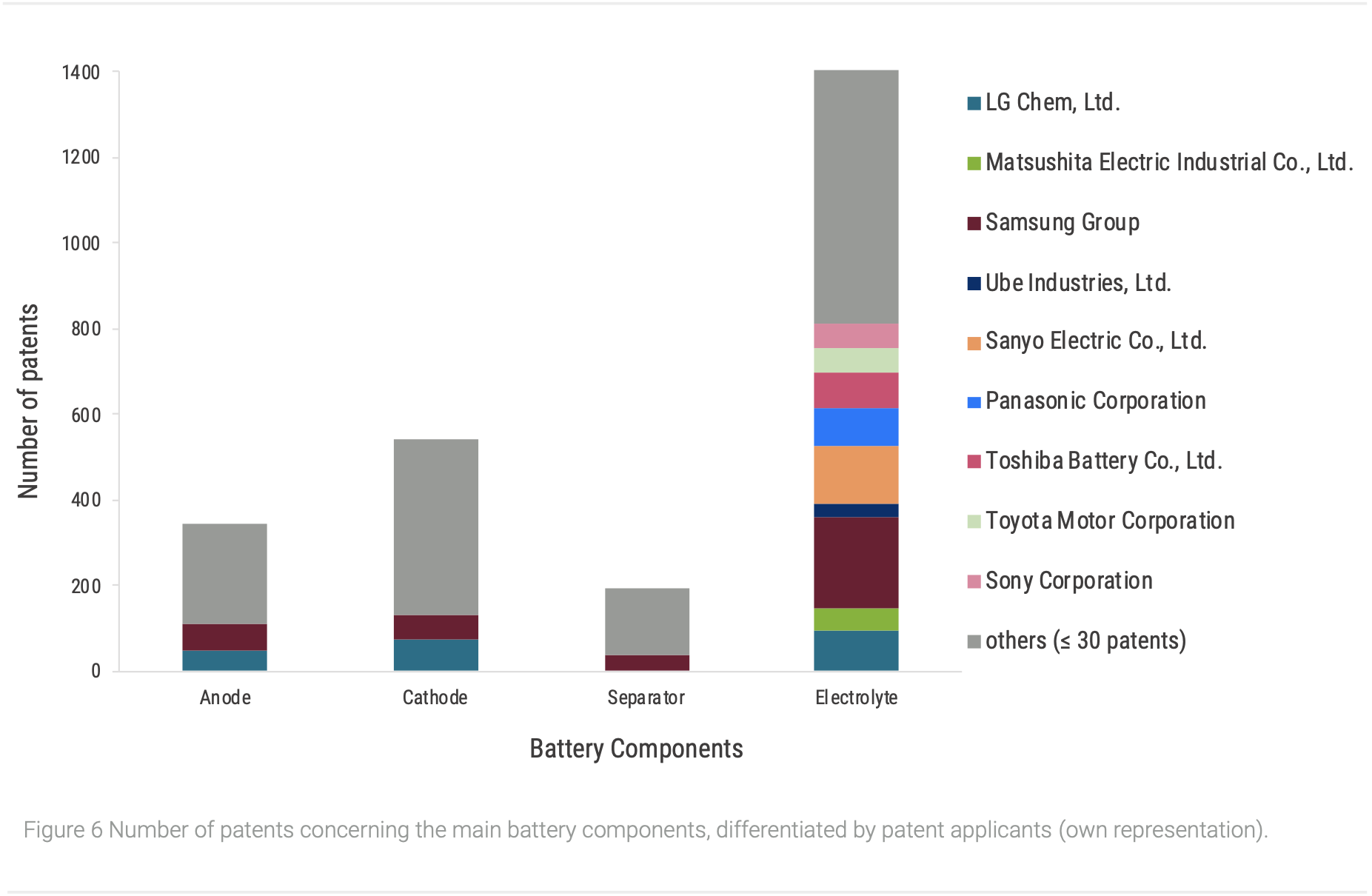
Generally, it can be observed, that the electrolyte is with over 1300 patents the most examined battery component, followed by the cathode (approx. 500 patents) and the anode (approx. 300 patents). With not even 200 patents the separator is investigated the least, indicating that it is the component with the lowest optimizing potential. Despite being a central element of the battery, the electrolyte-research has been neglected for a long time (Placke et al., 2017). Now with rising importance of high-performance batteries the electrolyte is analysed more extensively and market oriented, which is visible in the high patent numbers. An important research area is for example the development of solid electrolytes for solid-state batteries (Xiao et al., 2020). The big majority of patent holders are companies, which indicates highly market-oriented research. Especially the Lithium-ion battery (LIB) is on the market for several decades and exceeded the point of basic research. Big companies like Samsung possess over more financial assets than for example universities, which eases the patent application. Furthermore, patent applications are not common at many universities and are often not profitable (Geuna and Nesta, 2006).
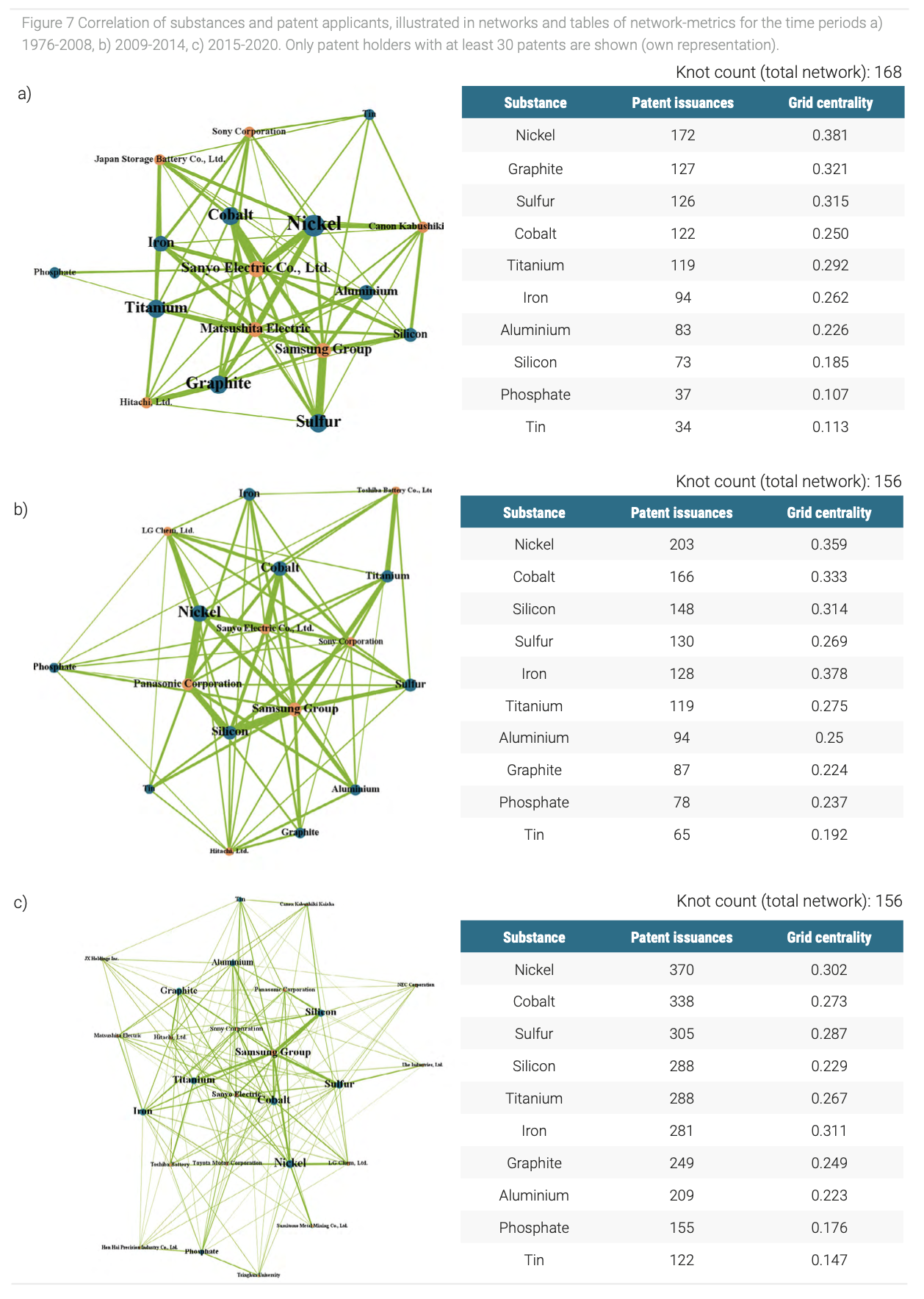
To further specify the technology analysis, we did a keyword-search in the patent abstracts for typical elements (despite lithium) and substances in lithium-based batteries, to observe the significance of specific substances in current research and development efforts (Figure 7). The extracted elements were assigned to the corresponding applicant and the visualisation of these connections enables to create a network that represents the relations between applicant and element. In it the nodes represent an applicant or an element and the connections or respectively edges represent the relation between them. The size of the nodes and edges is proportional to its occurrence. Besides the occurrence, network specific grid centrality values are used to investigate how dominant certain nodes are in the network. These values consider the amount and intensity of connections from a node to all other nodes in the network. To recognize changes and illustrate trends, we divided the patent landscape into the three time-periods 1976-2008 (Figure 7a), 2009-2014 (Figure 7b) and 2015-2020 (Figure 7c).
The increasing significance of batteries and the rising size of the patent-landscape can be abstracted from the development of the network size. With 341 knots (10 substances + 331 patent applicants) the current six-year period (2015-2020) more than doubles the size of the previous periods, despite the first periods longer time scale and the fact that 2020 is not finished yet. We investigated ten substances on their significance in terms of patent numbers. Conspicuous is, that for all three periods nickel is the substance with the highest number of patent issuances. An explanation is, that nickel-rich, high-energy cathodes are promising materials to develop LIBs with a high energy density (Xu et al., 2017), which are especially needed for electric cars. An interesting development can be observed for the anode-materials graphite and silicon. While in the first period graphite is ranked second after nickel, in the two following periods it is dropping to place eight and seven of the ranking. Graphite anodes are cheap, technologically mature and show a high cycling stability (Wagner et al., 2013), therefore they are currently implemented in nearly every LIB. The fact that their development is already very advanced can explain the declining significance as a research object and be an indicator for companies to avoid new investments in graphite-anode-research. The contrary development is visible for silicon. In the first period it is only positioned on the 8th place of the ranking. In the following two periods the number of patents is doubling respectively, and silicon ranks on the places three and four. Silicon is viewed as a promising future anode-material, for example the development of silicon-graphite-composite electrodes can lead to higher specific capacities compared to conventional graphite-anodes (Zuo et al., 2017). By examining the networks, the high patent numbers and the rise of silicon-research can mostly be allocated to increasing research activities of only a few companies, in particular Samsung, Panasonic, Sanyo and Sony. Generally, the networks vividly illustrate, on which substances specific companies are focussing their research, which eases an overview on this complex market. Thereby specialists, who focus strongly on one substance, like Toshiba on titanium can be distinguished from companies with a broader and more diversified research portfolio, like Samsung or Sony. Moreover, it is conspicuous that iron, for example part of the cathode in lithium iron phosphate batteries, has the highest grid centrality of all substances in the second and third period, but only an average number of patents. So, iron has the highest number of connections to different companies, but most companies only hold a small number of patents. A possible explanation could be that the research of the low-cost and abundant element is very diverse and leads to several different applications (Wang et al., 2012; Yabuuchi and Komaba, 2014). Since there is no big player, who is dominating the research yet, this could be an opportunity for companies to take advantage of this gap and invest in iron-based battery research.
The two analyses showed possibilities to structure, categorize, and quantify complex technology markets. Next to showing technology and research trends, especially the product and research portfolio of companies and competitors can be thoroughly analysed, deriving recommendations for specific actions and investments. As a result, insecurities about the technological strength of competitors and of own research-investments can be minimized.
3.4 Patent analysis of stem cells
In our last case study, we focus on interactions in a legally controversial area that is stem cell research. Stem cells are body cells that can develop into different cell types and have regenerative properties (Shen et al., 2004). The application of stem cells in human medicine promises the treatment of diseases like cancer, diabetes, or neurological diseases (Kim and De Vellis, 2009; Volarevic et al., 2011). Despite their broad applications and promising treatment options, stem cells are a much debated topic to their production. The most interesting stem cells for research are embryonic stem cells, because they are pluripotent and thus can develop into all cell types (Fernandes et al., 2009). However, these must be taken from embryos and then propagated in cell cultures (Richards et al., 2004). This led to ethical debates, which finally resulted in laws on the handling of stem cells in Germany, the USA and other countries. Based on these developments, the following two questions arise:
- Which actors have the greatest influence in the stem cell research?
- What are the most prominent technology classes?
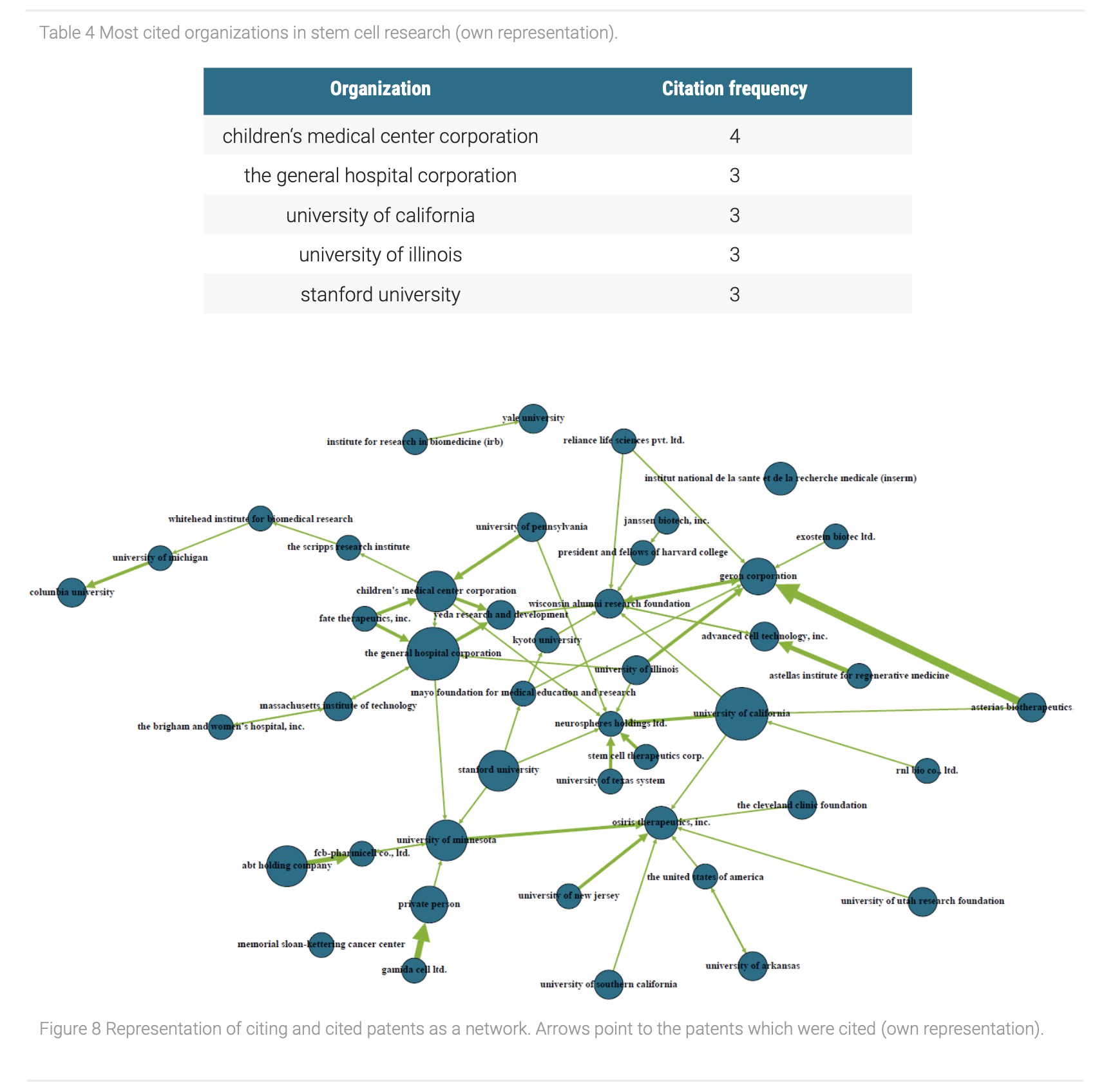
For the investigation of the influence of organizations in the stem cell research, we applied the network analysis similar to the battery case study, but this time connections between citing and cited patents were visualized. Therefore, the influence of an organization can be measured by investigating the extent of how often it was cited by others. Figure 8 shows an overview of the interaction of different applicants in the stem cell research field.
The size of the nodes is proportional to its citation frequency and the direction of the arrows on the edges show which organization have cited a patent from another applicant. Regarding the centrality measures, the most influential organizations of the network, which means the most cited patents, can be revealed (Table 4). From this it follows that universities such as the general hospital corporation, the university of California and the university of Illinois represent the holder of patents with the highest impact in the network. This is remarkable especially because the share of university institutions in the regarded data set is 24.44%. Therefore, this could be an indicator that universities play a central role in stem cell research. The reason for this could be the high quality of research or a specialization of universities in basic research. The focus on basic research can be further the reason for the high number of citations, as these patents could form the basis for other research projects. The situation that universities play the dominant role in the stem cell research may also result from the fact that the research field is at an early stage, which is why no or only few lucrative applications for the industry were developed yet. A Re: Journal of Business Chemistry neue Ausgabe Nummerierungen nother option could be that the government is imposing stronger regulations on research in companies and research at university institutions is partially exempt.
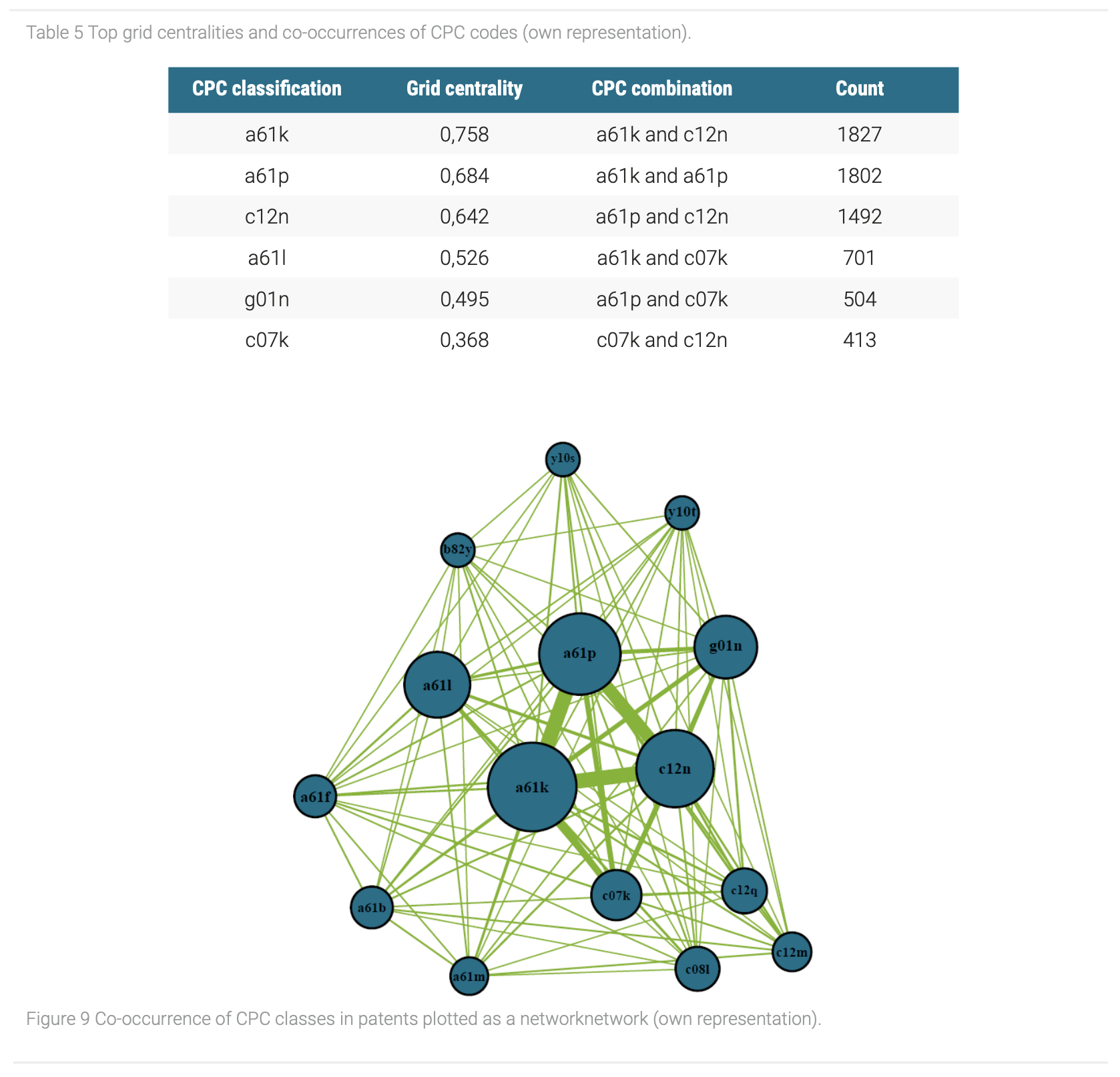
After finding out on which sources most patents are built, we took a look in which technology areas the most research is being done and how they are interconnected. For this purpose, the Cooperative Patent Classification (CPC) codes are investigated, which represent an extension of the IPC codes and enable insights in the most prominent technology areas in the stem cell research. Figure 9 shows a network with the most frequent CPC categories as nodes and its relations to each other as edges.
Regarding the network, five CPC classifications were highlighted through their size, which represent their frequency of occurrence in patents. Among these, the classifications a61k, a61p and c12n possess especially strong connections to each other (Table 5). This could indicate that these codes commonly occur together and most of the patents base on them. Therefore, it seems that the usage of microorganisms or respectively enzymes for medical purposes in form of therapies is the dominant application in the stem cell research (Table 6). Moreover, while the CPC code c07k, which stands for peptides, represent a less prominent classification in the patent data set due to its size, it possesses strong connections to the most frequent CPC codes a61k and a61p. It follows that the usage of peptides for medical purposes could be a smaller field in the stem cell area. However, this could be a hint for a growing application field in the stem cell research that will gain great importance in the future.
Through the visualization of different aspects of patent data with the network analysis the key player and key technology areas with their relationship with each other in the stem cell research could be identified. Therefore, the development stage of the research field can be estimated. This could support investment decisions due to a better understanding in how far the transition from basic research to applied research has already been proceeded. The visualization of the influence of organizations is further useful to find valuable cooperation partners or respectively acquisition targets. Moreover, by visualizing technology areas focus and emerging topics of the research field can be grasped, whereby decision makers may decide if the research field is lucrative or if there are research gaps that could be exploited.
4 Discussion
The application of data science methods on patent data from different industries showed that patent data holds a great variety of information, which allow to analyze the business environment from different perspectives. This can quickly build a data-based understanding of the environment but also allows to monitor developments in industries even with simple data science methods that can support decision making. Moreover, this article showed that patent data represent a valuable information source for companies. Analyzing information sources such as scientific publications or social media can also contribute to the understanding of the business environment. On the one hand, scientific publications hold information about the most recent research in an industry. Therefore, research trends can be grasped in an early stage, which could build the foundation for innovations and patents. Scientific publications are also similar to patents in that they must go through a review process and thus the information is thoroughly checked before publication. Thereof it results that they also represent a high-quality source of information. On the other hand, social media data could represent the social opinion on specific topics and may deliver information about trends in that area. The opinion of the society can also play an important role in many industries. Ethical concerns like in the stem cell research can hamper a field of research, although it is a promising field. This leads to consequences for future research and products. The advantage but also disadvantage of social media is that nowadays everyone is able due to smart devices to produce content in the internet. Therefore, a great amount of information is produced every day, but this information is not validated by anyone, whereby the quality of the content can vary. Nevertheless, it follows that multiple source should be considered to grasp different aspects of the business environment and be able to understand the big picture. However, we decided to use patent data because, apart from their information content, they offer a particular advantage to the user. The structure of patents, which consists of unstructured as well as structured parts, simplifies the analysis of this information source. Scientific publications or social media data such as tweets mainly consists of text, which represents unstructured data. The analysis of this data type is usually more complex, because texts generally have a high proportion of unimportant content. As a result, the analysis requires a lot of effort to clean the data in order to obtain high quality results. This, in turn, requires the user to engage more intensively with the field of data science. Furthermore, the interpretation of textual analyses is not always intuitive. For instance, while a word count allows easily identifying strongly represented topics as keywords in a dataset, performing and evaluating a network analysis on a text involves more difficulties. Patents, however, possess structured information that can be easily modified and interpreted without much prior knowledge, which was shown in the case studies. In addition, the wide range of information types, such as application date, applicant, CPC codes, offers the possibilities to analyze many different aspects, whereby the consideration of multiple information types in one context greatly expands the possibilities for analyses with data science methods.
For instance, the analysis of the development of patent applications over the years allowed us to get a first overview of an industry. Therefore, its maturity stage can be derived by investigating if the number of applications is still rising, stagnating, or falling. This development is a picture of the s-curve, which represents a typical course of technologies and could give evidence about how much potential a technology has left or respectively how satisfied a market is. The development can also be divided between different technologies of a market to get information about the potential of specific technologies, which was shown in the antibiotics market. This close look at a market by differentiating its technologies is particularly important to find out whether the market is generally developing positively but also whether, despite a negative development, technologies with high potential can be found in which it would be worthwhile to invest.
Combining the information of the number of patent application with names of the applicants offered us a new perspective on the patent landscape. While we figured out before how the whole industries developed, we could now find out who the key players are by analyzing which organizations hold the most patents. The type of organizations can thereby also give hints at which maturity stage a market stands. On the one hand, a strong presence of university institutions may rather represent an early stage, where the market is more focused on basic research and has no or few lucrative applications for companies. On the other hand, a strong presence of companies could lead to the recognition that the field is already well understood in the industry, which is why it has distanced itself from the basic research in universities and instead research is applied in the companies itself. Knowing who the key players are is further a necessary information to understand the competitive environment and therefore to localize valuable cooperation partners or respectively in some cases acquisition targets. Another perspective on the players in an industry can be taken by analyzing citation information from patent data. Whereas in the analyses before the strongest companies were determined according to the number of patent applications, their influence could be grasped by combining the information of citing and cited patents as well as the names of the patent holders. From this, frequently cited patents could represent patents with a high impact, which build the bases for further technologies. This impact is afterwards attributed to the patent applicant and could also give evidence about the maturity stage of the technology. As we have seen it in the stem cell research case, a high influence of university institutions could point to a strong presence of basic research. Furthermore, frequently cited patents reveal where most high quality and trend-setting knowledge in this area is available or respectively is generated, which are important strategic information for companies.
However, the patent analysis not only enable to reveal the key players in a whole industry, but also to break down complex industry environments, whereby organizations can be allocated to specific segments. This was shown in case 3, where the battery market was analyzed. We had the opportunity to analyze, which organizations dominate the whole battery market, but we divided the market by the battery components. Therefore, on the one hand the distribution of the companies in the industry could be visualized, whereby electrolytes were revealed as the most prominent segment. On the other hand, for each part of the industry the specific competitive environment could be investigated. Depending on which segment a company is targeting, direct competitors and cross-segment cooperation can be localized. Following, analyzing patents with data science methods enable to reduce complex industry structures, what makes it possible to get a better understanding of the environment through a more detailed overview.
Here, data science enables to combine different information, whereby various contexts can be investigated. Aside from the ability to view different pieces of information together in a new context, data science also offers the ability to present these analyses differently. Therefore, this also allows results to be viewed from different angles, expanding the possibilities for evaluation. Visualizing the organizations with the most cited patents as a ranking has the advantage that quickly the most influent ones can be highlighted. However, by plotting the results as a network, such as in the stem cell research case, the way we look at it changed. It enabled to see besides the most cited patent holder, the interactions and therefore the relations among them. This results in an ecosystem, which present the environment of companies. The monitoring of this ecosystem over time can represent changes in the environment of a company and therefore give an overview how relations among organizations emerge, change, or disappear. This procedure can also be applied to other cases in order to investigate other types of relations, such as the relationships between technology areas in form of CPC codes to investigate how they are related to each other. Here, data science again shows its advantages by making it possible to analyze multiple attributes in one context. This allows to investigate connections of varying complexity. Analyzing single attributes such as citations showed us which organization influenced another one. The analysis of linkages between two different attributes like chemical elements and organizations like in the third case offered new insights. In that analysis the usage of prominent chemical elements in the battery industry was the focus. On that basis, companies can be compared to each other, which sheds new light on the competitive environment. Depending on the focus of the company, various types of interactions in the environment can be investigated.
The high information content and analysis potential of patents are the reason why many different advanced analysis approaches have been developed over time to gain more and better insights into the business environment. Aaldering et al. (2019) developed a patent-based approach, which aims to assist R&D efforts by predicting technological knowledge interaction trajectory. This approach uses the network analysis to identify and quantify links between interacting technological knowledge areas in form of IPC codes. Based on that analysis link prediction technique is used to predict emerging, decaying and changing relation between knowledge areas in the future. Aaldering and Song (2019) extended this approach by also analyzing the descriptive text passages of the patents. Descriptive parts of patents can define knowledge areas more precisely than IPC codes by using technical terms. Therefore, they could extract the exact application fields of different battery technologies such as vehicles, devices, energy storage and computers, whereby new findings about the trajectory of application-oriented research could be gained. While most of the technological information of patents is found in the texts, their analysis offers many new possibilities. For instance, Wang et al. 2010 applied text analysis methods to derive information about future trends from descriptive text. In contrast, Yoon et al. (2013) created a text analysis approach to build dynamic patent maps, which reveal information about competition trends and technological developments. Finally, patent analysis represents a highly researched field, since its diverse information content allows the application of many different methods. The popularity of this analysis also stems from the fact that the complexity is variable. As this article showed, patent analysis can be performed quite simply to obtain strategic information. However, by combining different complementary methods, the analysis can be made arbitrarily complex to obtain even deeper insights into the corporate environment.
5 Conclusion and limitations
Although we only scratched the surface of data science methods here, we were able to gain deep insights into various industries. These simple methods enabled us to quickly build up an understanding of developments in the industries. Thus, we were able to analyze the markets from different perspectives without much prior knowledge. One of the biggest advantages of data science is that once the methods were developed, they can be applied on every data set without much effort. This makes it easier to monitor developments in the patent landscape so that an understanding of the environment and potential changes or respectively trends can be built. Also, companies can increase the quality of their decisions by leveraging data, as well as make strategic decisions with some foresight. Remarkable is that these knowledge could be derived by only analyzing patent data as information source. This means that important strategic information, which could grant competitive advantages is freely available for anyone. In addition, the simplicity and efficiency of patent analysis was made clear in this article. For these reasons, an awareness for the possibilities that arise from data science methods and the growing amount of free available data must be created in companies in order to understand the increasingly complex environment and to survive in the future.
Even though patents have been presented here as a valuable source of information, this type of data has certain limitations. It must be considered that not all inventions were applied as patents. Some are kept as company secrets because the inventors do not want to reveal their invention. Also, international differences in patent law hardens the comparison of patents from different places. This is also leading to a different acceptance of patent applications. At last, it must be considered that there is a delay in time between the application and the acceptance, which results in a distortion of the actuality. Despite these limitations patent analysis plays nowadays an important role for decision-making in many companies, which will probably gain greater importance in the future.
References
Aaldering, L. J., Leker, J., Song, C. H. (2019): Competition or collaboration?–analysis of technological knowledge ecosystem within the field of alternative powertrain systems: a patent-based approach, in: Journal of cleaner production, 212, pp. 362-371.
Aaldering, L. J., Song, C. H. (2019): Tracing the technological development trajectory in post-lithium-ion battery technologies: A patent-based approach, in: Journal of Cleaner Production, 241, pp. 118-343.
Achilladelis, B., Antonakis, N. (2001): The dynamics of technological innovation: the case of the pharmaceutical industry, in: Research Policy 30(4), pp. 535–588.
Allahyari, M., Pouriyeh, S., Assefi, M., Safaei, S., Trippe, E. D., Gutierrez, J. B., Kochut, K. (2017): A brief survey of text mining: Classification, clustering and extraction techniques, Preprint at ArXiv:1707.02919, pp. 1-13.
Aydogan, N. (2009): Innovation Policies, Business Creation and Economic Development: A Comparative Approach, 1, New York: Springer.
Birnbaum, J., Kahan, F. M., Kropp, H., Macdonald, J. S. (1985): Carbapenems, a new class of beta-lactam antibiotics: discovery and development of imipenem/cilastatin, in: The American journal of medicine, 78(6), pp. 3-21.
Bonino, D., Ciaramella, A., Corno, F. (2010): Review of the state-of-the-art in patent information and forthcoming evolutions in intelligent patent informatics, in: Technovation, 23, pp. 1-13.
Brynjolfsson, E., Hitt, L. M., Kim, H. H. (2011): Strength in numbers: How does data-driven decisionmaking affect firm performance? SSRN Workingpaper, available at SSRN: http://ssrn.com/abstract=1819486.
Chan, I. S., Ginsburg, G. S. (2011): Personalized medicine: progress and promise, in: Annual review of genomics and human genetics, 12, pp. 217–244.
Cukier, K. (2010): Data, data everywhere: A special report on managing information, in: Economist Newspaper, (27 February 2010), pp. 1-14.
Davis, J. C., Furstenthal, L., Desai, A. A., Norris, T., Sutaria, S., Fleming, E., Ma, Philip (2009): The microeconomics of personalized medicine: today‘s challenge and tomorrow‘s promise, in: Nat Rev Drug Discov 8 (4), pp. 279–286.
Day, G. S., & Schoemaker, P. J. H. (2004): Driving through the fog: managing at the edge, in: Long Range Planning, 37(2), pp. 127–142.
Deutsches Patent- und Markenamt (2018): Jahresbericht 2018, München: DPMA.
Din, A. I. (1994): Structured query language (SQL) A practical Introduction, 1, Oxford: Blackwell.
Dou, H., Leveillé, V., Manullang, S., Dou Jr, J. M. (2005): Patent analysis for competitive technical intelligence and innovative thinking, in: Data Science Journal, 4, pp. 209-237.
Dreßler, A. (2006): Patente in technologieorientierten Mergers & Akquisition, Wiesbaden: Deutscher Universitäts-Verlag.
Ernst, H. (2003): Patent information for strategic technology management, in: World patent information, 25, pp. 233-242.
Fernandes, T. G., Diogo, M. M., Clark, D. S., Dordick, J. S., Cabral, J. M. (2009): High-throughput cellular microarray platforms: applications in drug discovery, toxicology and stem cell research, in: Trends in biotechnology, 27(6), pp. 342-349.
Geuna, A., Nesta, L. J.J. (2006): University patenting and its effects on academic research: The emerging European evidence, Research Policy, 35(6), pp. 790–807.
Green, E. D., Guyer, M. S. (2011): Charting a course for genomic medicine from base pairs to bedside, in: Nature, 470(7333), pp. 204-213.
Hancock, R. E. (1997): Peptide antibiotics, The lancet, 349(9049), pp. 418-422.
Haupt, R., Kloyer, M., Lange, M. (2007): Patent indicators for the technology life cycle development, in: Research Policy 36(3), pp. 387–398.
Hentschel, M. (2007): Patentmanagement, Technologieverwertung und Akquise externer Technologien, Wiesbaden: Deutscher Universitäts-Verlag.
Holman, C. M. (2015): The Critical Role of Patents in the Development, Commercialization and Utilization of Innovative Genetic Diagnostic Test and Personalized Medicine, in: B.U. J. Sci. & Tech. L. 21, 297, available online: https://heinonline.org/HOL/Page?handle=hein.journals/ jstl21&id=315&div=17&collection=journals.
Katz, M. L., Mueller, L. V., Polyakov, M., & Weinstock, S. F. (2006): Where have all the antibiotic patents gone? in: Nature biotechnology, 24(12), pp. 1529-1531.
Kayser, V. (2016): Extending the knowledge base of foresight. Dissertation, Fakultät VII – Wirtschaft und Management, Technische Universität Berlin, Berlin.
Kim, S. U., De Vellis, J. (2009): Stem cell‐based cell therapy in neurological diseases: a review, in: Journal of neuroscience research, 87(10), pp. 2183-2200.
Kroker, M. (2015): Big Data: 2,5 Trillionen Byte Daten jeden Tag, wächst vier Mal schneller als Weltwirtschaft, URL: https://blog.wiwo.de/look-at-it/2015/04/22/big-data-25-trillionen-byte-daten-jeden-tag-wachst-vier-mal-schneller-als-weltwirtschaft/, Latest access: 28.01.2021.
Lee, H., Smith, K. G., Grimm, C. M. (2003): The effect of new product radicality and scope on the extent and speed of innovation diffusion, in: Journal of Management, 29(5), pp. 753–768.
Lee, C., Kim, J., Kwon, O., Woo, H-G. (2016): Stochastic technology life cycle analysis using multiple patent indicators, in: Technological Forecasting and Social Change, 106, pp. 53–64.
Mohrman, K., Ma, W., Baker, D. (2008): The Research University in Transition: The Emerging Global Model, in: High Educ Policy, 21(1), pp. 5–27.
Mutschler, E., Geisslinger, G., Kroemer, H. K., Schäfer-Korting, M. (2001): Arzneimittelwirkung – Lehrbuch der Pharmakologie und Toxikologie, 8, Stuttgart: Wissenschaftliche Verlagsgesellschaft.
NDR (2019): Antibiotika-Forschung: Warum Unternehmen aussteigen, URL: https://www.ndr.de/ratgeber/gesundheit/Antibiotika-Forschung-Warum-Unternehmen-aussteigen,antibiotika586.html, Latest access: 29.01.2021.
Park, H., Kim, K., Choi, S., Yoon, J. (2013): A patent intelligence system for strategic technology planning, in: Expert Systems with Applications, 40, pp. 2373-2390.
Parry, M. E., Song, M., De Weerd‐Nederhof, P. C., Visscher, K. (2009): The impact of NPD strategy, product strategy, and NPD processes on perceived cycle time, in: Journal of Product Innovation Management, 26(6), pp. 627–639.
Placke, T., Meister, P., Rothermel, S., Bar, A., Wedel, W. v. (2017): Elektromobilität – Was uns jetzt und künftig antreibt: Batterie-, Brennstoffzellen- und Hybridantrieb, BINE Informationsdienst.
Qualls, W., Olshavsky, R. W., Michaels, R. E. (1981): Shortening of the PLC: An Empirical Test, in: Journal of Marketing, 45(4), pp. 76-80.
Reitzig, M. (2004): Strategic Management of Intellectual Property, in: MIT Sloan Management Review, 45, pp. 35-40.
Rice, M. (2019): 17 Data Science Applications & Examples, URL: https://builtin.com/data-science/data-science-applications-examples, Latest access: 28.01.2021.
Richards, M., Tan, S. P., Tan, J. H., Chan, W. K., Bongso, A. (2004): The transcriptome profile of human embryonic stem cells as defined by SAGE, in: Stem cells, 22(1), pp. 51-64.
Samuels, M. (2017): Big data case study: How UPS is using analytics to improve performance, URL: https://www.zdnet.com/article/big-data-case-study-how-ups-is-using-analytics-to-improve-performance/, Latest access: 28.01.2021.
Scrosati, B., Garche, J. (2010): Lithium batteries: Status, prospects and future, in: Journal of Power Sources, 195(9), pp. 2419–2430.
Shen, Q., Goderie, S. K., Jin, L., Karanth, N., Sun, Y., Abramova, N., Vincent, P., Pumiglia, K., Temple, S. (2004): Endothelial cells stimulate self-renewal and expand neurogenesis of neural stem cells, in: Science, 304(5675), pp. 1338-1340.
Siwczyk, Y. (2010): IT-gestützte White-Spot-Analyse, Stuttgart: Frauenhofer.
Smith, M., Hansen, F. (2002): Managing intellectual property: a strategic point of view, in: Journal of Intellectual Capital, 3, pp. 366-374.
Song, C. H. (2015): Früherkennung von konvergierenden Technologien: ein neuer Ansatz zur Identifikation attraktiver Innovationsfelder, Wiesbaden: Springer-Verlag.
Song, C. H., Han, J.-W., Jeong, B., Yoon, J. (2017): Mapping the Patent Landscape in the Field of Personalized Medicine, in: J Pharm Innov, 12(3), pp. 238–248.
Sood, A., Tellis, G. J. (2005): Technological evolution and radical innovation, in: Journal of Marketing, 69(3), pp. 152–168.
Tanwar, M., Duggal, R., Khatri, S. K. (2015): Unravelling unstructured data: A wealth of information in big data, in: Proceedings of the 2015 4th International Conference on Reliability, Infocom Technologies and Optimization (ICRITO) (Trends and Future Directions), Noida, pp. 1–6.
Thielemann, A., Neef, C., Fenske, C., Wietschel, M. (2018): Energiespeicher-Monitoring 2018: Leitmarkt- und Leitanbieterstudie: Lithium-Ionen-Batterien für die Elektromobilität, Fraunhofer-Institut für System- und Innovationsforschung ISI.
Toole, A. A. (2007): Does Public Scientific Research Complement Private Investment in Research and Development in the Pharmaceutical Industry? in: The Journal of Law and Economics, 50(1), pp. 81–104.
Volarevic, V., Arsenijevic, N., Lukic, M. L., Stojkovic, M. (2011): Concise review: mesenchymal stem cell treatment of the complications of diabetes mellitus, Stem cells, 29(1), pp. 5-10.
Wagner, R., Preschitschek, N., Passerini, S., Leker, J., Winter, M. (2013): Current research trends and prospects among the various materials and designs used in lithium-based batteries, in: Journal of Applied Electrochemistry, 43(5), pp.481-496.
Wang, M. Y., Chang, D. S., Kao, C. H. (2010): Identifying technology trends for R&D planning using TRIZ and text mining, in: R&d Management, 40(5), pp.491-509.
Wang, H., Liang, Y., Gong, M., Li, Y., Chang, W., Mefford, T., Zhou, J., Wang, J., Regier, T., Wei, F., Dai, H. (2012): An ultrafast nickel-iron battery from strongly coupled inorganic nanoparticle/nanocarbon hybrid materials, in: Nature Communications, 3(1), pp. 917.
WIPO (2019): WIPO IP Facts and Figures 2019, Geneva: WIPO.
Xiao, Y., Wang, Y., Bo, S. H., Kim, J. C., Miara, L. J., Ceder, G. (2020): Understanding interface stability in solid-state batteries, in: Nature Reviews Materials, 5(2), pp. 105-126.
Xu, J., Lin, F., Doeff, M. M., Tong, W. (2017): A review of Ni-based layered oxides for rechargeable Li-ion batteries, in: Journal of Materials Chemistry A, 5(3), pp. 874–901.
Yabuuchi, N., Komaba, S. (2014): Recent research progress on iron- and manganese-based positive electrode materials for rechargeable sodium batteries, in: Science and Technology of Advanced Materials, 15(4), pp. 43501.
Yoon, J., Park, H., Kim, K. (2013): Identifying technological competition trends for R&D planning using dynamic patent maps: SAO-based content analysis, in: Scientometrics, 94(1), pp. 313-331.
Zuo, X., Zhu, J., Müller-Buschbaum, P., Cheng, Y.‑J. (2017): Silicon based lithium-ion battery anodes: A chronicle perspective review, in: Nano Energy, 31, pp. 113–143.